1.5 Kangaroo 物理引擎
Created on 2024-08-31T13:22:52+08:00 @author: Richie Bao
Kangaroo 是 GH 内部的一个物理引擎（physics engine），如图 1.5-1，用于交互模拟、形式发现、优化和约束求解等。
图 1.5-1 Kangaroo2 组件
🍋🟩代码段-练习-1: （ ）
建立一个平面格网，用MeshCorners提取格网角点，用Anchor组件固定这4个角点。通过控制点寻找到格网中的最近点，用组件Anchor控制该点（输入端 Point）到指定的目标点（输入端Target）。用组件Length(Line)调整线段的“弹性”，用Mesh Edges组件提取边，区分内外线段分别控制“弹性”大小。使用Solver组件解算。
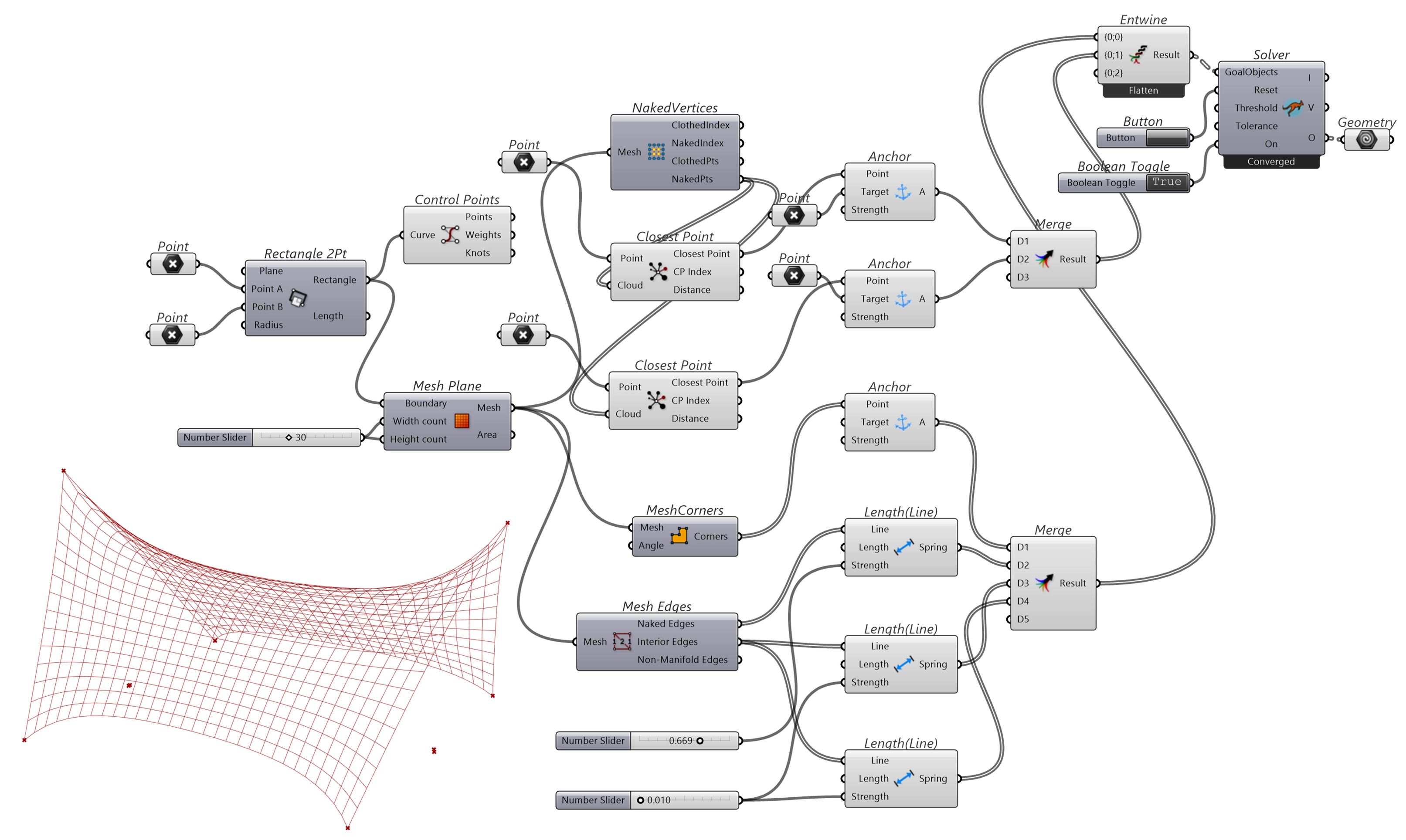
图 1.3.3-2 代码段（Kangaroo）-1与结果
⇩代码下载（codeSnippet_kangaroo_01.gh）
🍋🟩代码段-练习-2: （ ）
首先用Populate Geometry和Populate 2D组件生成的少数几个随机点用Delaunay Mesh构建父类的格网，以便用Anchor固定这几个控制点束缚格网。进而用Weaverbird's Split Triangles Subdivision组件（需要按照 Weaverbird 扩展插件）细分格网（子类）。用Show显示解算后要查看的对象，该案例为细分后的格网。用EdgeLengths调整格网所有单元边线的“弹性”（松弛格网），其输入端的控制参数包括LengthFactor，为控制目标边为当前边的一个倍数，及强度值Strength。Pressure会对格网施加一个模拟的压力，即向格网单元面（三边面）法向（垂直于面）施加一个力，与当前三边面的面积成正比。SphereCollide组件可以避免格网顶点的交织膨胀，是通过控制顶点各个虚拟球体的碰撞实现。
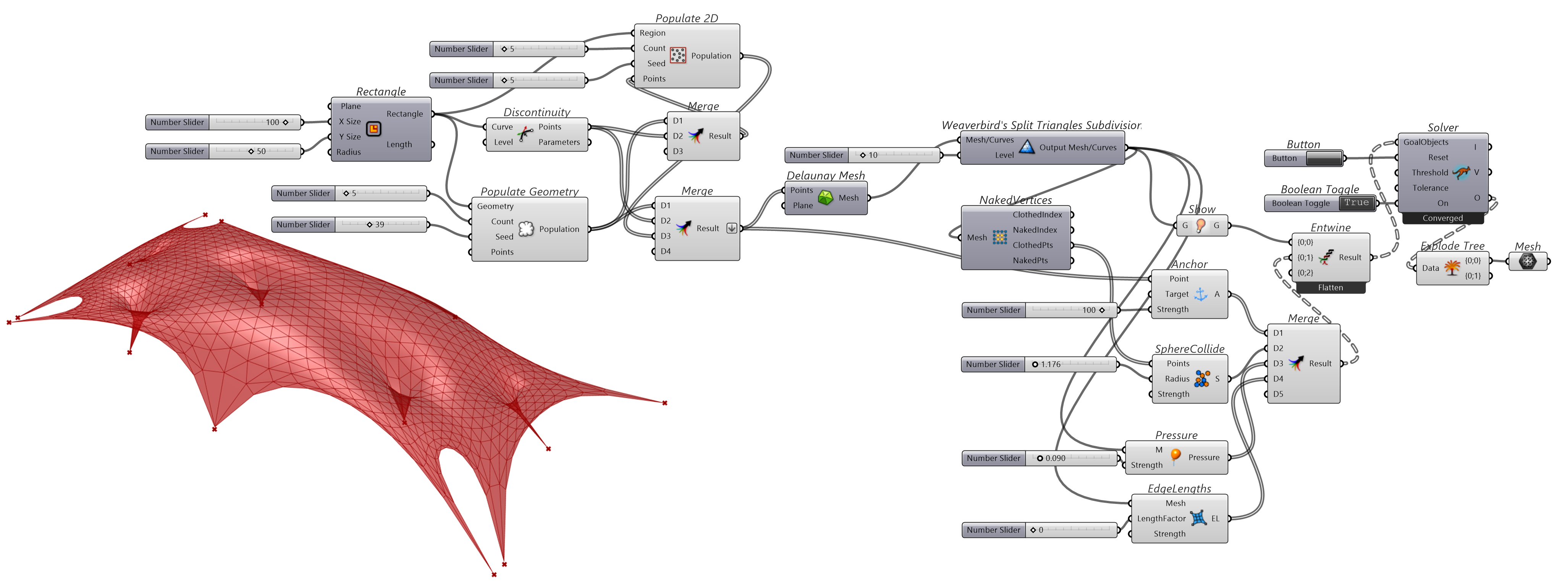
图 1.3.3-3 代码段（Kangaroo）-2与结果
⇩代码下载（codeSnippet_kangaroo_02.gh）
🍋🟩代码段-练习-3: （ ）
如果格网单元为三边面，那么该面一定为平面，但是如果为四边面则不一定为平面。为了使得使用四边面构建的对象单元为一个平面，方便实际的加工建构，可以用Planarize组件使其趋于平面化。平民化过程中必然会变动当前格网顶点的位置，使用PlasticAnchor组件提供的方法在给定的约束距离内（Limit）偏移顶点。底部和拱形边缘的顶点需要用Anchor固定，以防发生位移。同时用ClampLength组件控制四边面边线长度变化的范围。用EqualLength组件尽量使四边面单元面的对角线长度相等，即尽量让单元面为规整的矩形。Smooth用于光滑格网。而Grab组件则可以在 Rhino 空间中拖动顶点（通常按住左键拖动），改变几何对象形态。
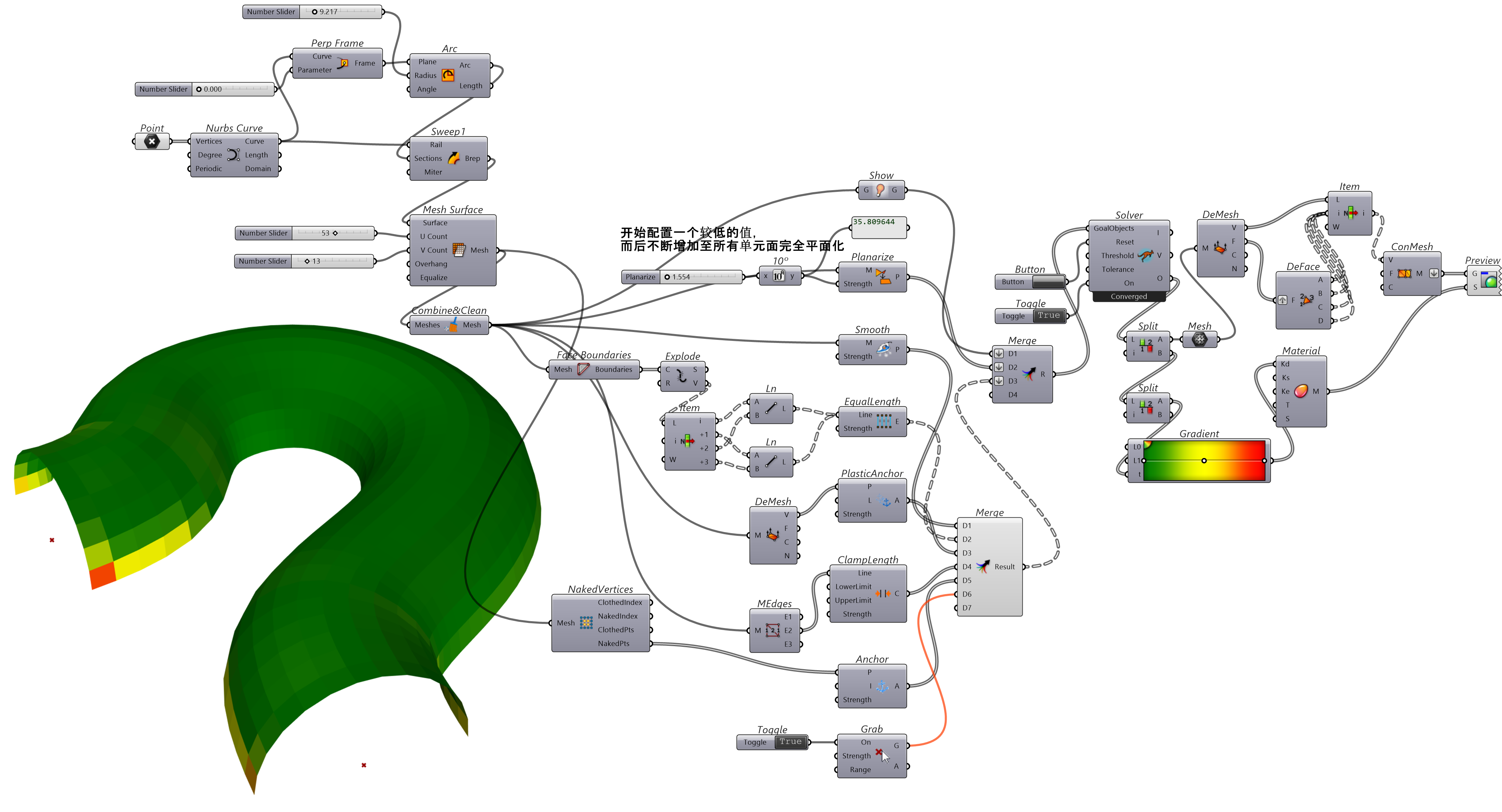
图 1.3.3-4 代码段（Kangaroo）-3与结果
⇩代码下载（codeSnippet_kangaroo_03.gh）
🍋🟩代码段-练习-4: （ ）
用Anchor组件固定住立方体格网的8个顶点，用EdgeLengtsh松弛格网，用Show组件显示解算后的几何对象，可以构建一个类似弹性材料包裹体拉伸的效果。
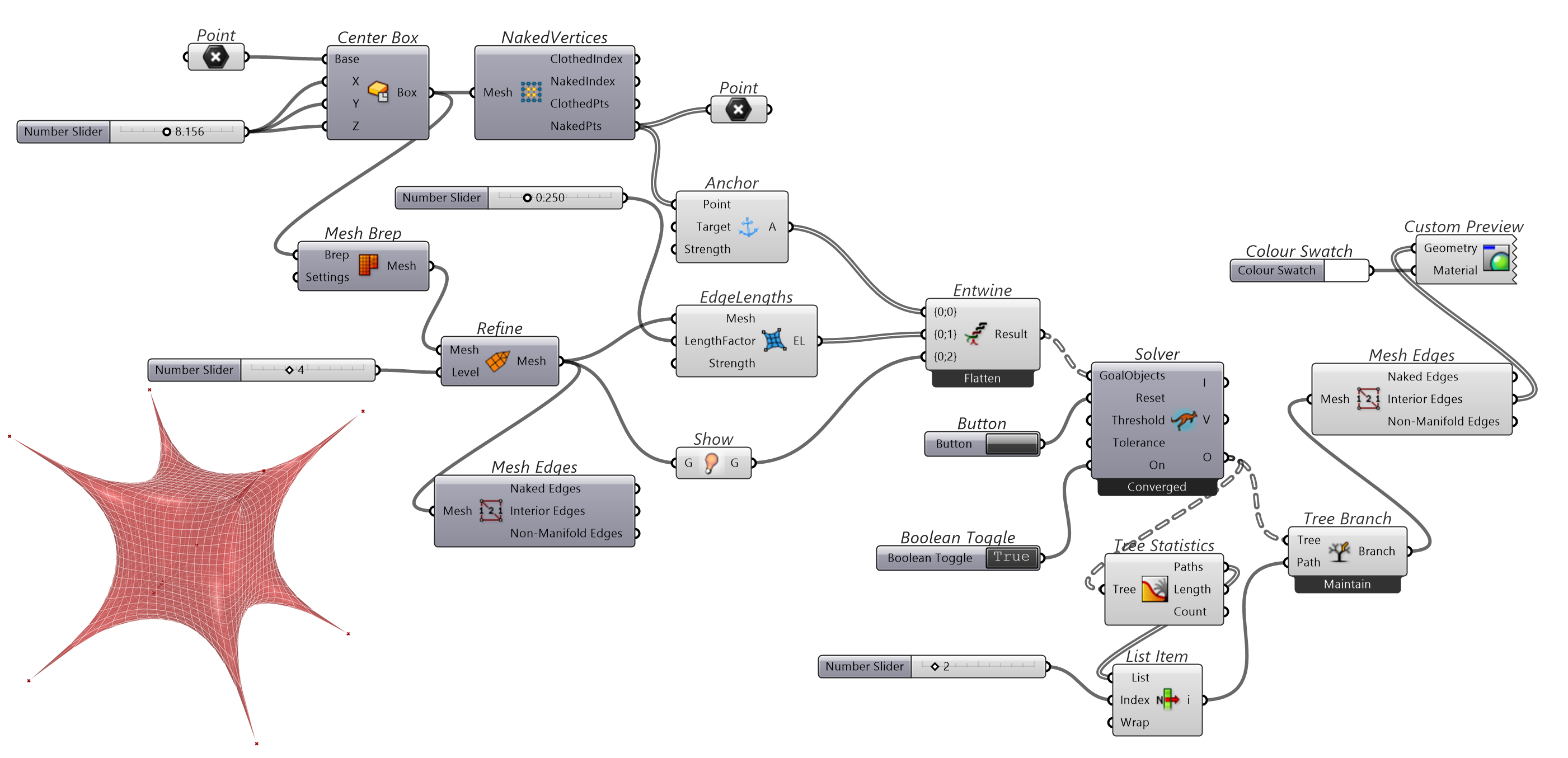
图 1.3.3-5 代码段（Kangaroo）-4与结果
⇩代码下载（codeSnippet_kangaroo_04.gh）
🍋🟩代码段-练习-5: （ ）
处理格网时经常用到Weaverbird①扩展插件，其主要组件如下：
Catmull-Clark smoothing (Weaverbird's Catmull-Clark Subdivision) |
计算由 Edwin Catmull 和 Jim Clark 首先在 1978 年描述的基于网格的递归细分类型。 生成的网格总是由四边面组成 |
Split mesh into Quads (Weaverbird's Constant Quads Split Subdivision) |
计算一个由四边面组成的新网格，是通过为原始网格任何一边添加一个面来获得 |
Loop smoothing (Weaverbird's Loop Subdivision) |
计算 Charles Loop 在 1987 年的数学论文中描述的基于网格的递归细分类型。生成的网格总是三边面组成 |
Split mesh with inner face (Weaverbird's Split Triangles Subdivisions) |
在每个面中置入几个三边面 |
Sierpinsky Triangles subdivision (Weaverbird's Sierpinski Triangles Subdivision) |
在网格的每个角上置入一个三边面。网格每面将至少存有一个孔洞 |
Frame (Weaverbird's Picture Frame) |
计算一个具有更高裸边数的新网格。其中每个面在中心有一个孔洞，类似于一个相框。生成的网格总是由四边面组成 |
Carpet (Weaverbird's Sierpinski Carpet) |
计算一个具有更高裸边数的新网格。其中每个面在中心有一个孔洞。 生成的网格总是由四边面组成 ，并且可以用于计算 Sierpinski 斑纹 |
Window (Weaverbird's Mesh Window) |
替换每个原始网格面为一个新的，并在内部重建。每个面与原来的面有相同数量的边 |
Weaverbird's Mesh Prism
Weaverbird's Mesh Antiprism
Weaverbird's Mesh Pyramid
Weaverbird's Mesh Dipyramid |
基本网格定义 |
用 Weaverbird 的Weaverbird's Mesh Mesh Icosahedron组件定义一个基本格网，并用Weaverbird's Loop Subdivision递归细分格网。用Volumne组件调整格网的体积变化，用Smooth平滑格网，用SphereCollide(SC)控制格网顶点之间的距离，并用Length(LIne)限制格网边的长度变化，会模拟球状格网“泄气”的形态变化。
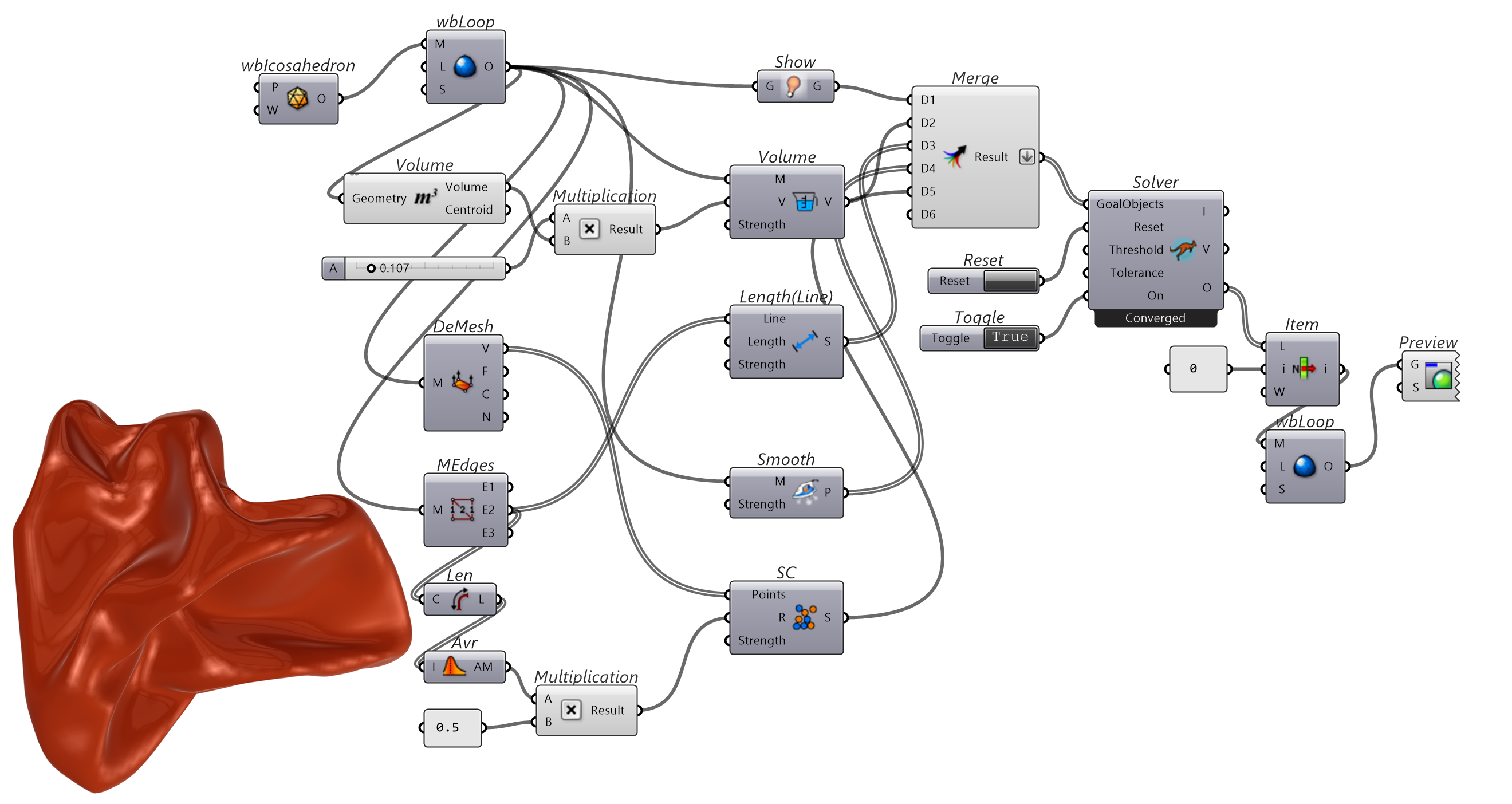
图 1.3.3-6 代码段（Kangaroo）-5与结果
⇩代码下载（codeSnippet_kangaroo_05.gh）
🍋🟩代码段-练习-6: （ ）
变化用Voronoi 3D生成的三维泰森多边形，用Anchor固定角点，用removeDuplicateLines组件移除叠合重复的线段，用Length(Line)变化各个泰森多边形边的长度，其输入端Length参数为原线段长度的倍数。
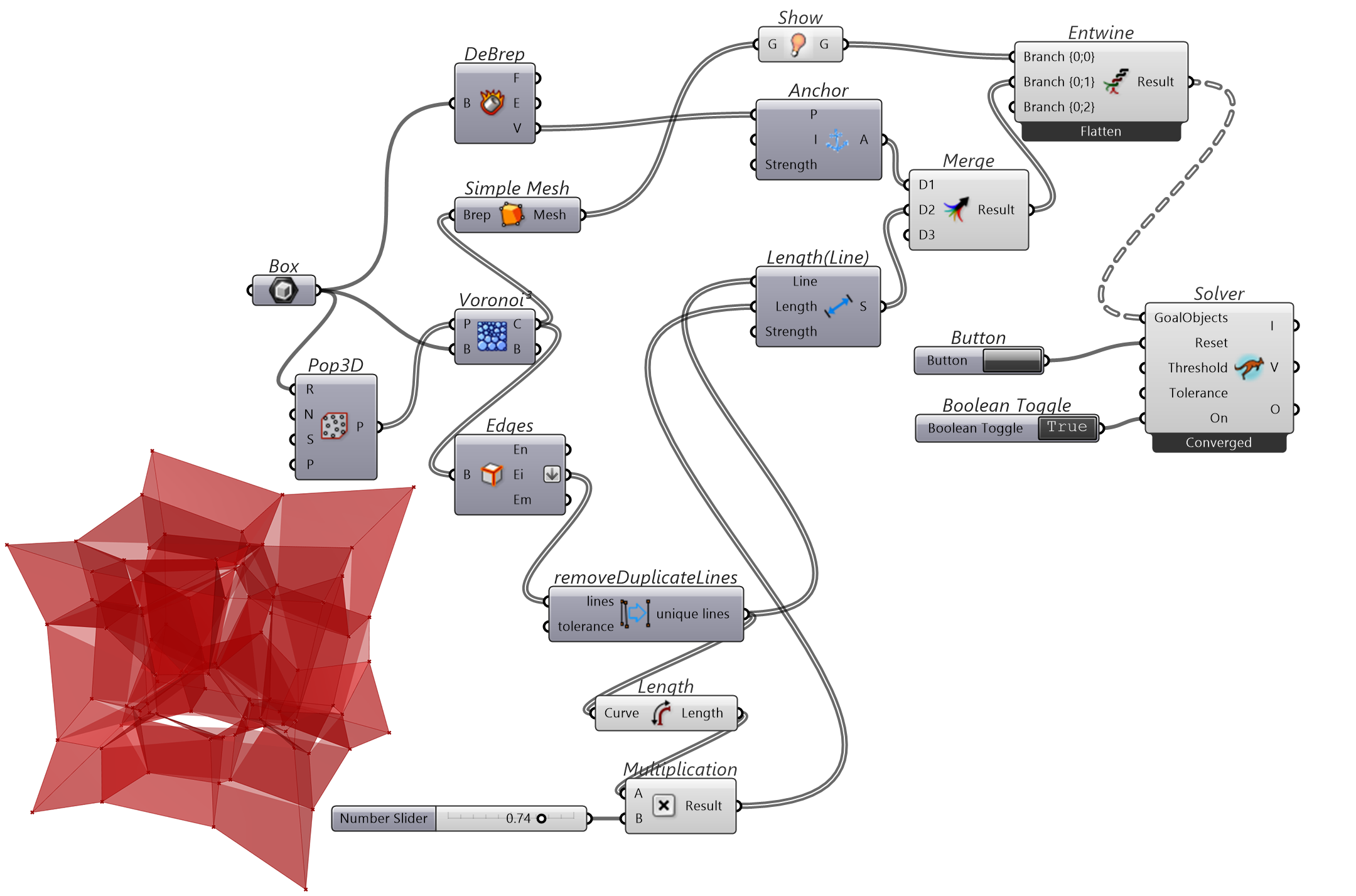
图 1.3.3-7 代码段（Kangaroo）-6与结果
⇩代码下载（codeSnippet_kangaroo_06.gh）
🍋🟩代码段-练习-7: （ ）
该代码段与代码段-3类似，用EqualLength组件分别控制格网内部边线和“碗口”裸露边线等长的强度，对“碗口”边线两两邻接边线施加一个Angle组件的角度限制。因为要拖曳格网达到雕刻的目的，对顶点施加PlasticAnchor，以便顶点能够在给定的阈值内移动，并用ClampLength限制边长的变化区间，增加Grab组件使得可以在 Rhino3D 空间拖曳格网顶点变化形态。
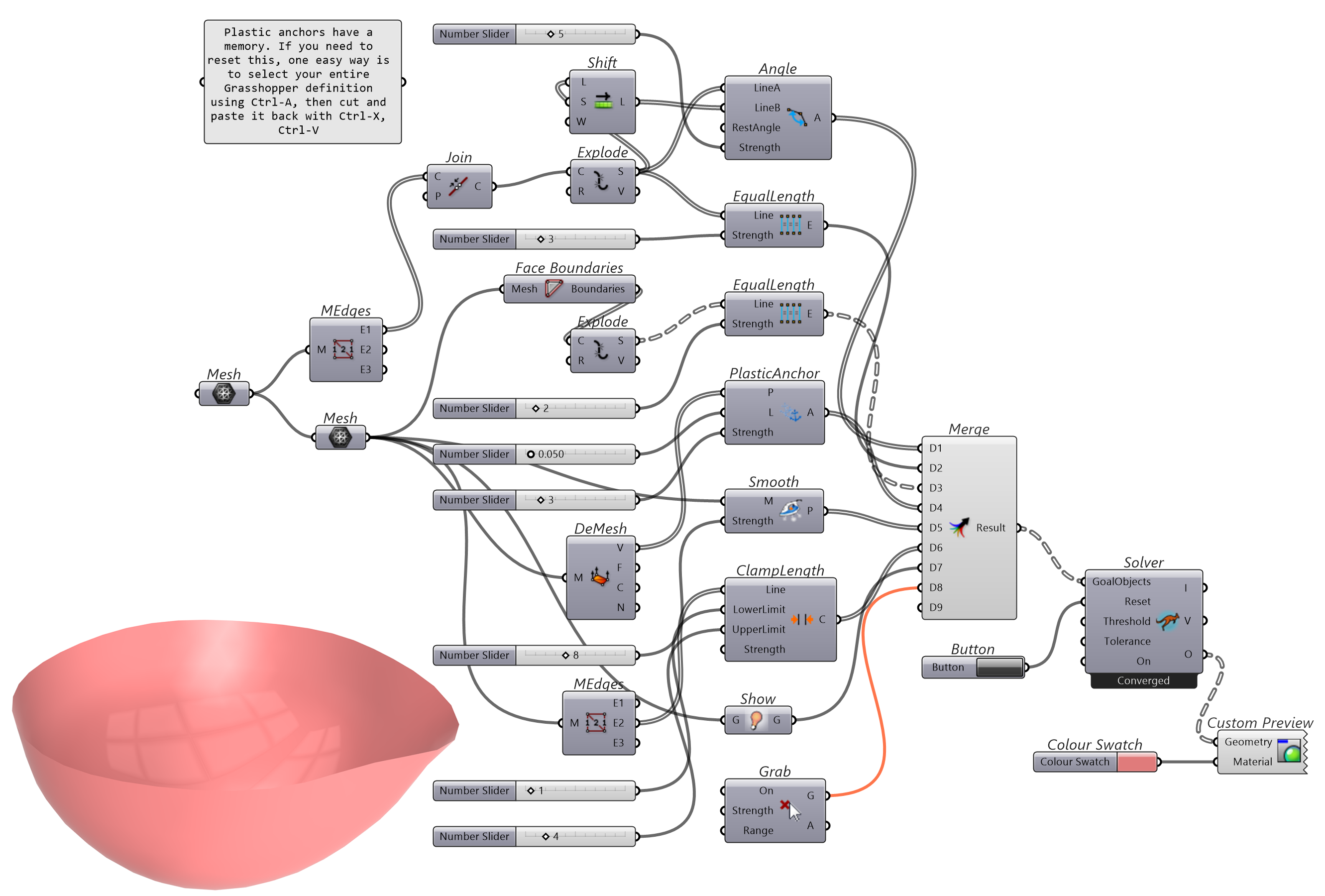
图 1.3.3-8 代码段（Kangaroo）-7与结果
⇩代码下载（codeSnippet_kangaroo_07.gh）
🍋🟩代码段-练习-8: （ ）
这是物体碰撞模拟，核心组件是使用Floor作为地面，限制物体通过；用Collider模拟加粗线段和球体之间的碰撞，并用Length(Line)保持线段的长度，且用Load施加一个模拟的重力，让物体自由落体并发生碰撞。
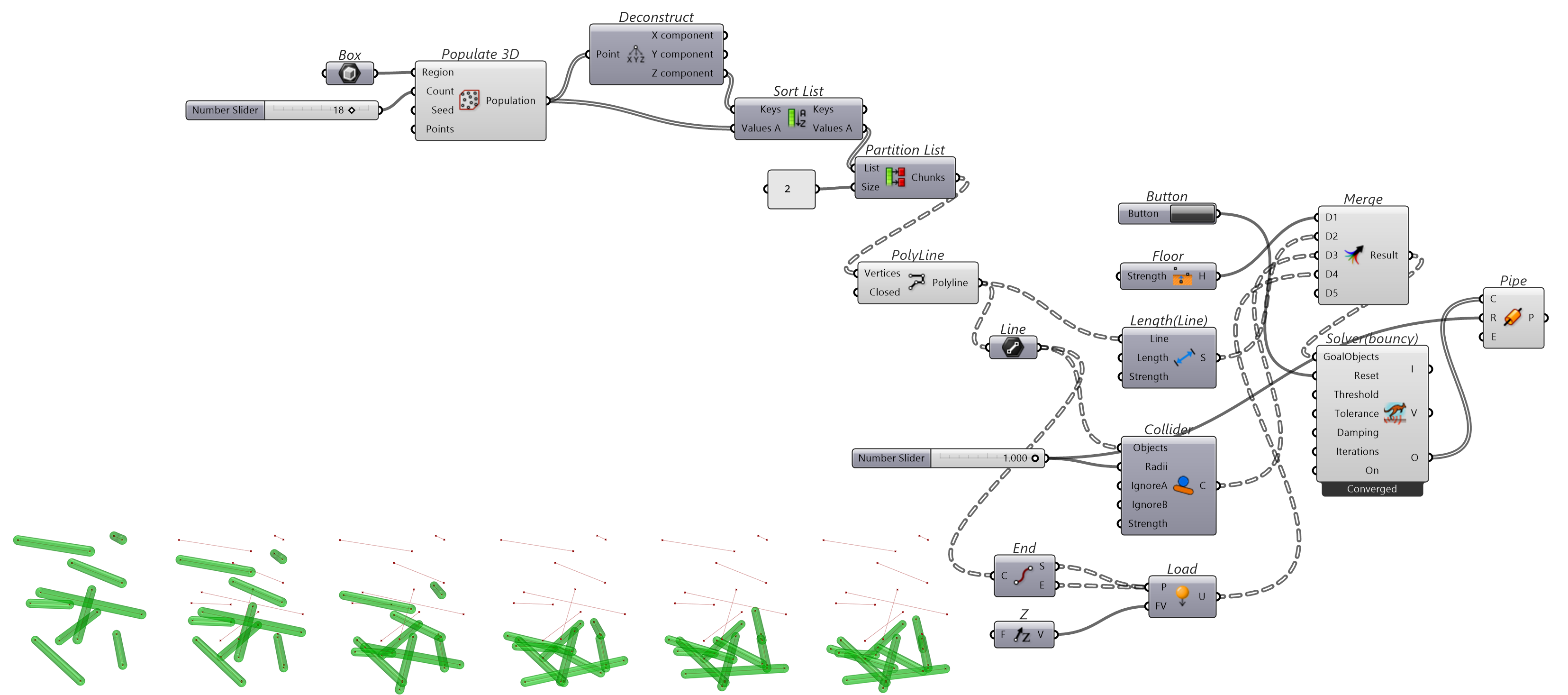
图 1.3.3-9 代码段（Kangaroo）-8与结果
⇩代码下载（codeSnippet_kangaroo_08.gh）
🍋🟩代码段-练习-9: （ ）
SphereCollide和OnMesh组件配合，可以控制顶点在格网面上移动，并彼此之间保持给定参数Radius(r)半径的距离，从而达到基于解算后的顶点，新建几何对象（例如圆）贴附于格网表面并彼此间保持距离或相互贴合。
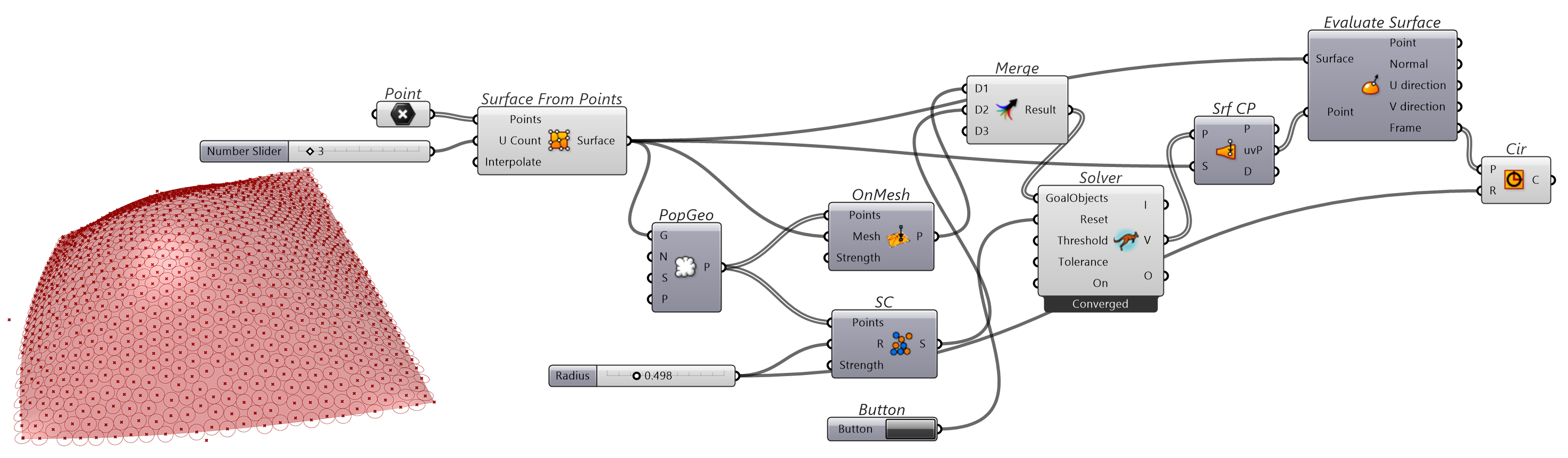
图 1.3.3-10 代码段（Kangaroo）-9与结果
⇩代码下载（codeSnippet_kangaroo_09.gh）
🍋🟩代码段-练习-10: （ ）
SolidPointCollide组件可以控制输入端Points对象是否被挡于Solid对象之外，能够用于模拟点（粒子）对象碰撞的行为。用Floor模拟地面行为，用SphereCollide组件控制粒子间的距离。
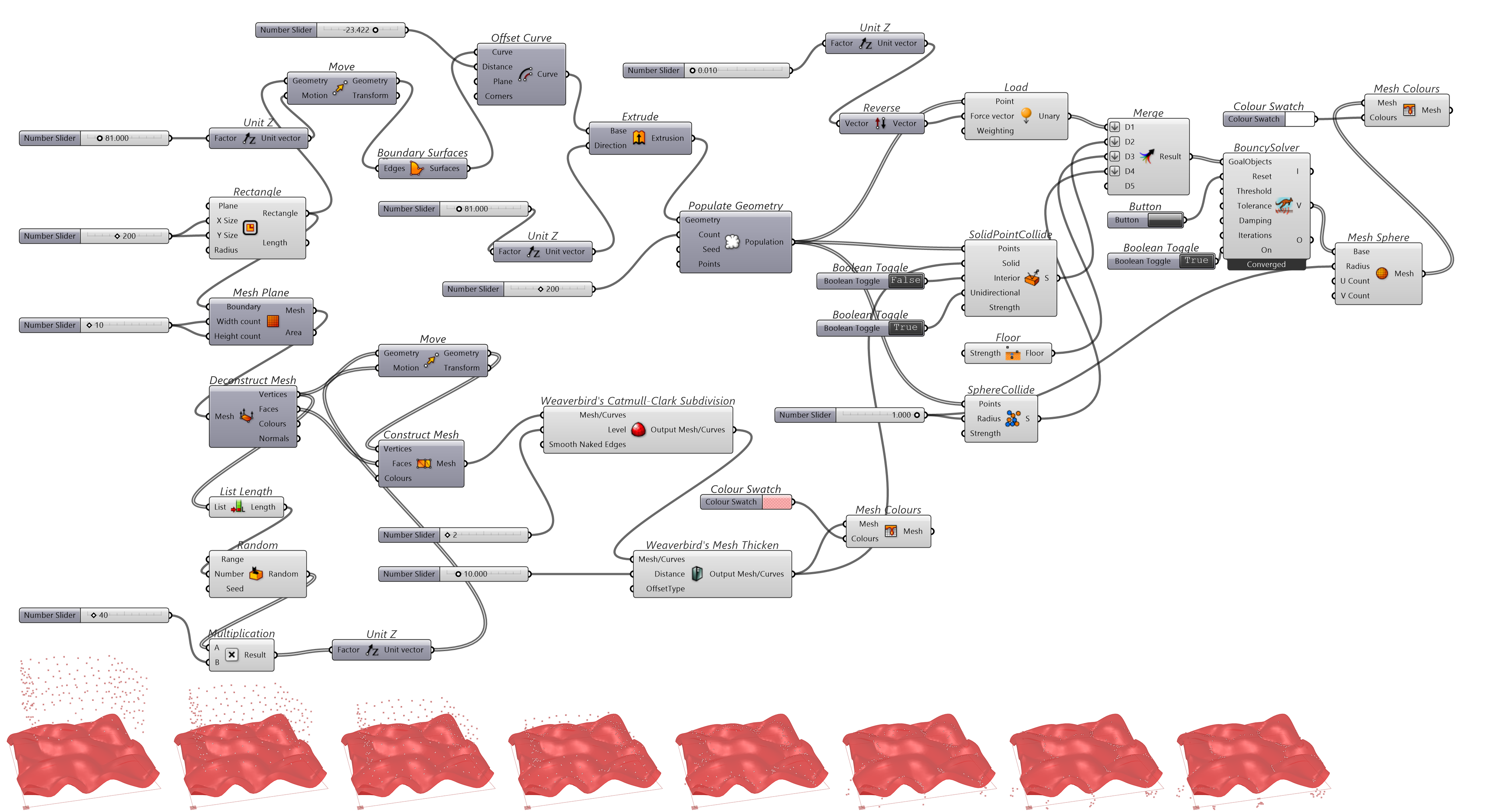
图 1.3.3-11 代码段（Kangaroo）-10与结果
⇩代码下载（codeSnippet_kangaroo_10.gh）
🍋🟩代码段-练习-11: （ ）
将一个圆切分成无数线段，用Lengh(Line)控制这些线段的长度，用SphereCollide控制点之间的距离，用PlasticAnchor约束原始的等分点，使得点（粒子）自由的向圆外扩散，拟合出多样的形态。
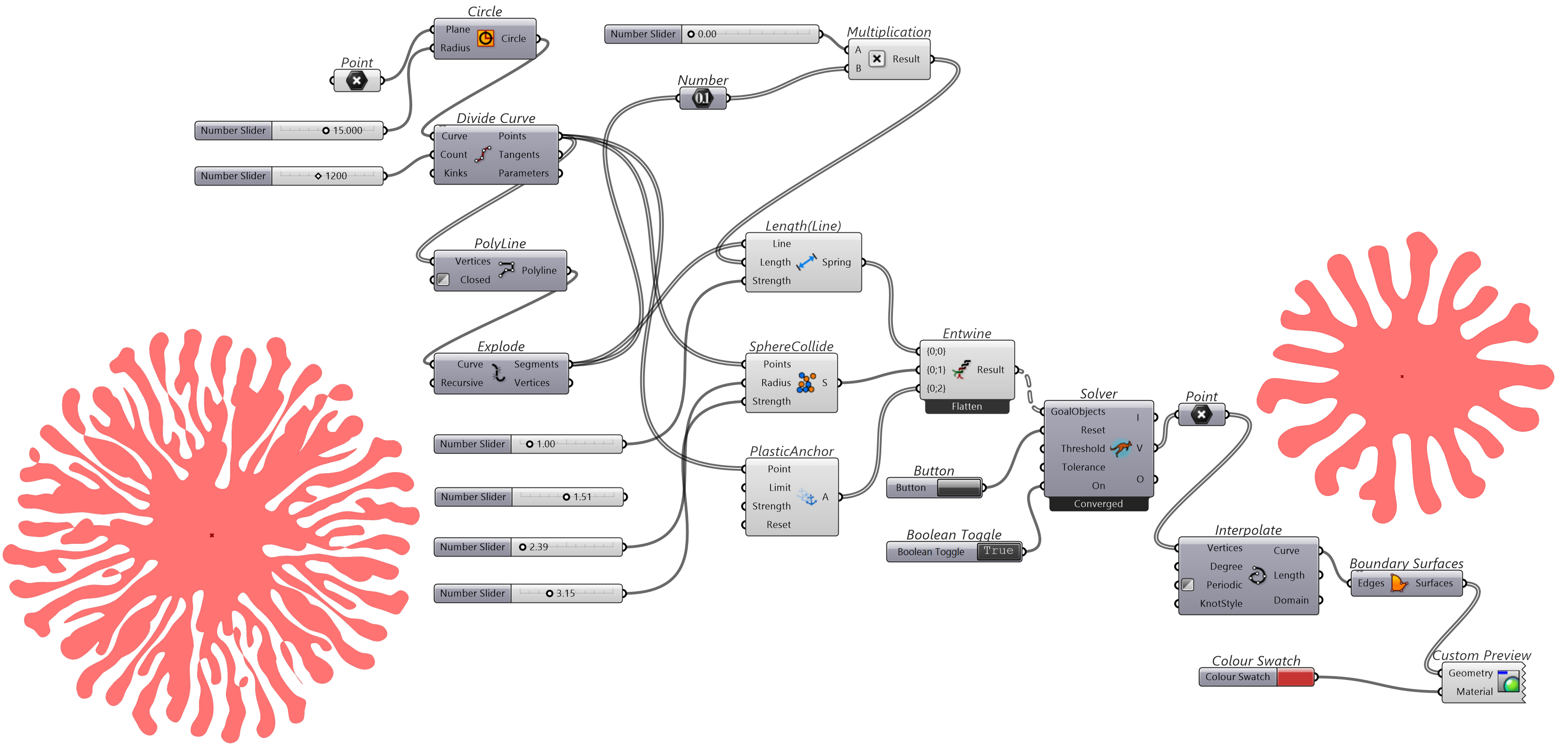
图 1.3.3-12 代码段（Kangaroo）-11与结果
⇩代码下载（codeSnippet_kangaroo_11.gh）
🍋🟩代码段-练习-12: （ ）
基于一个平面格网，用Anchor固定住指定的少数几个格网顶点拴住变化的格网，用EdgeLengths松弛格网单元的边线，并控制沿边（裸露）的顶点在发生位置改变时用AnchorXYZ组件固定其 X 和 Y 值，保持水平位置不变而仅变化 Z 值，因此可以观察到沿边顶点为垂直位移。
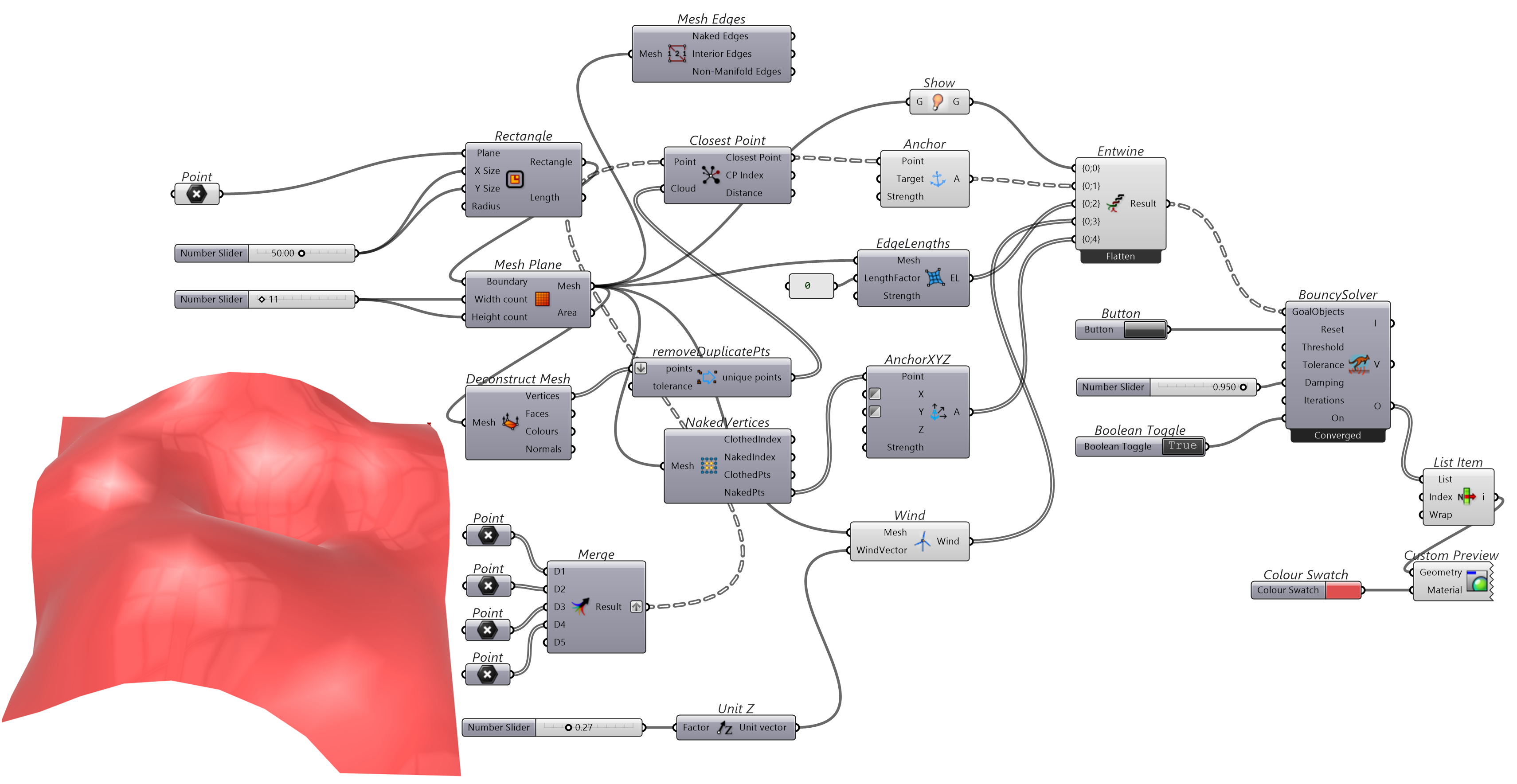
图 1.3.3-13 代码段（Kangaroo）-12与结果
⇩代码下载（codeSnippet_kangaroo_12.gh）
🍋🟩代码段-练习-13: （ ）
与代码段-11 基本同，只是增加了OnMesh 将粒子的移动贴附于给定的球体表面。
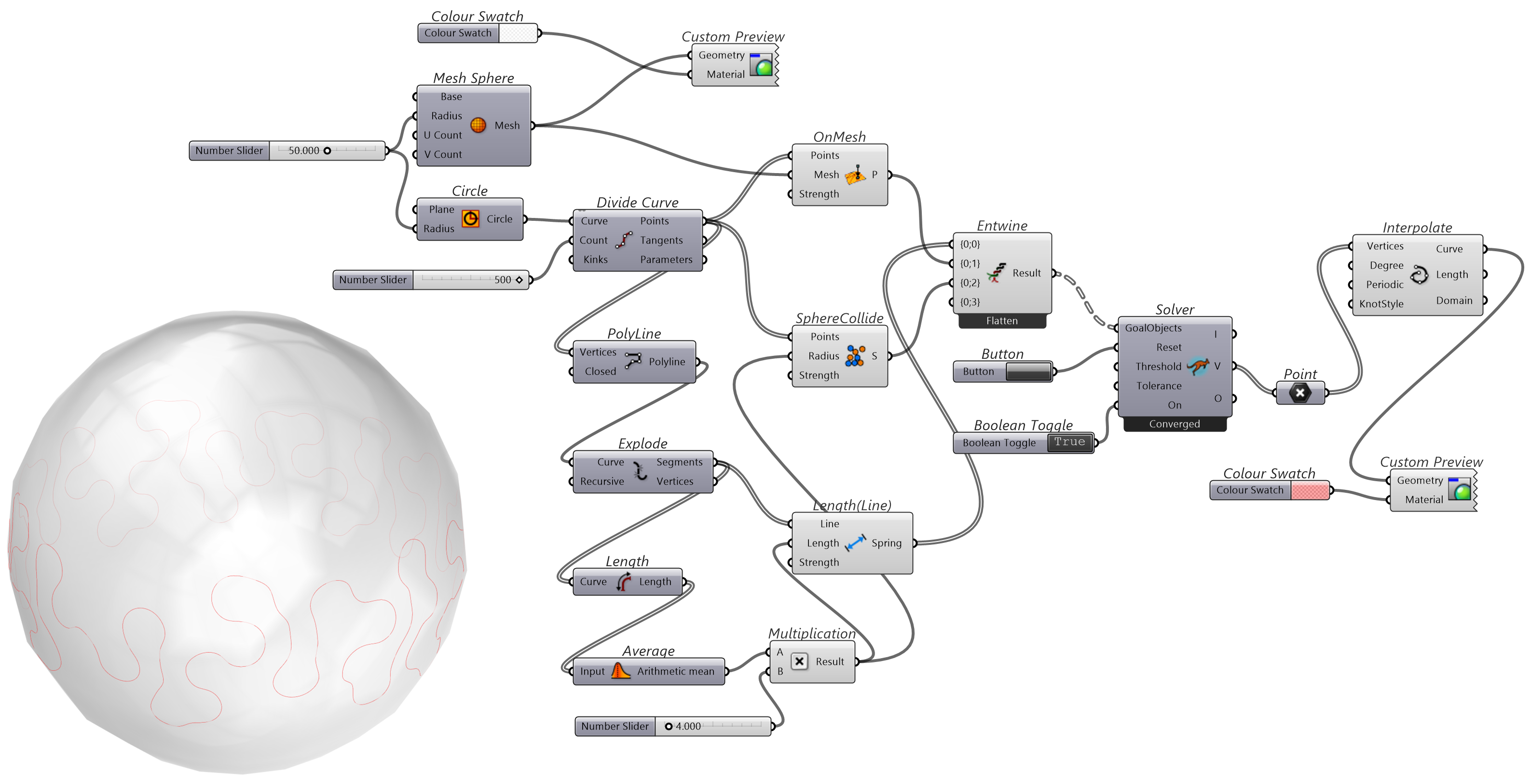
图 1.3.3-14 代码段（Kangaroo）-13与结果
⇩代码下载（codeSnippet_kangaroo_13.gh）
🍋🟩代码段-练习-14: （ ）
基本思路与代码段-1，2，12 等相同，给定一个类似空间管状的格网，用Anchor固定裸露的边缘顶点到各自参考平面绘制的圆的最近点映射上，并用EdgeLength松弛格网边线。
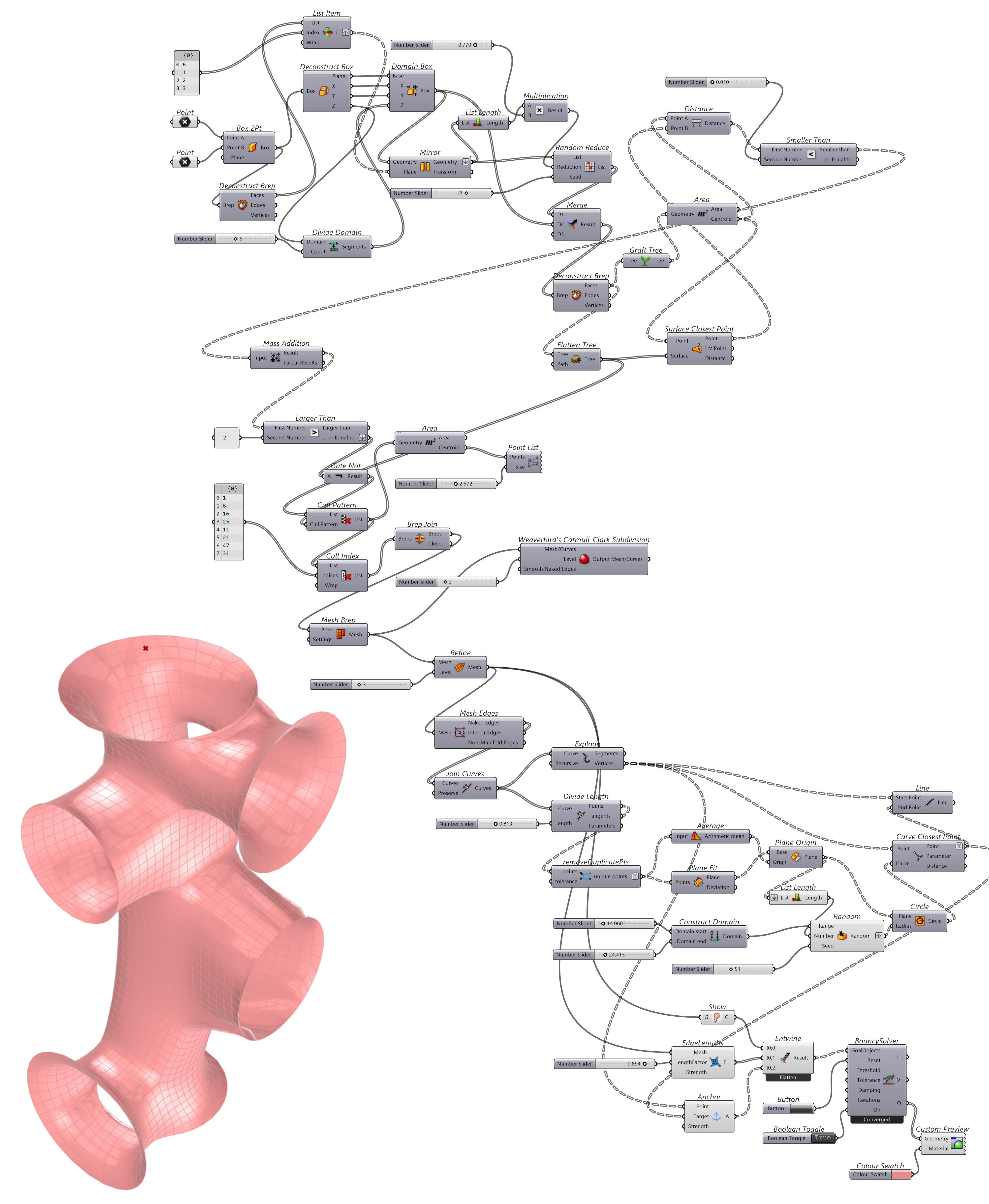
图 1.3.3-15 代码段（Kangaroo）-14与结果
⇩代码下载（codeSnippet_kangaroo_14.gh）
🍋🟩代码段-练习-15: （ ）
该代码段为模拟折纸，用Length(Line)保持格网单元面的边长保持不变，即纸张不会发生变形；用Floor模拟地面，使得格网（纸张）似乎位于一个桌面上；用Hinge铰链沿“折痕”模拟合页的开合；并用Load施加力使得“纸张”沿“折痕”转动。
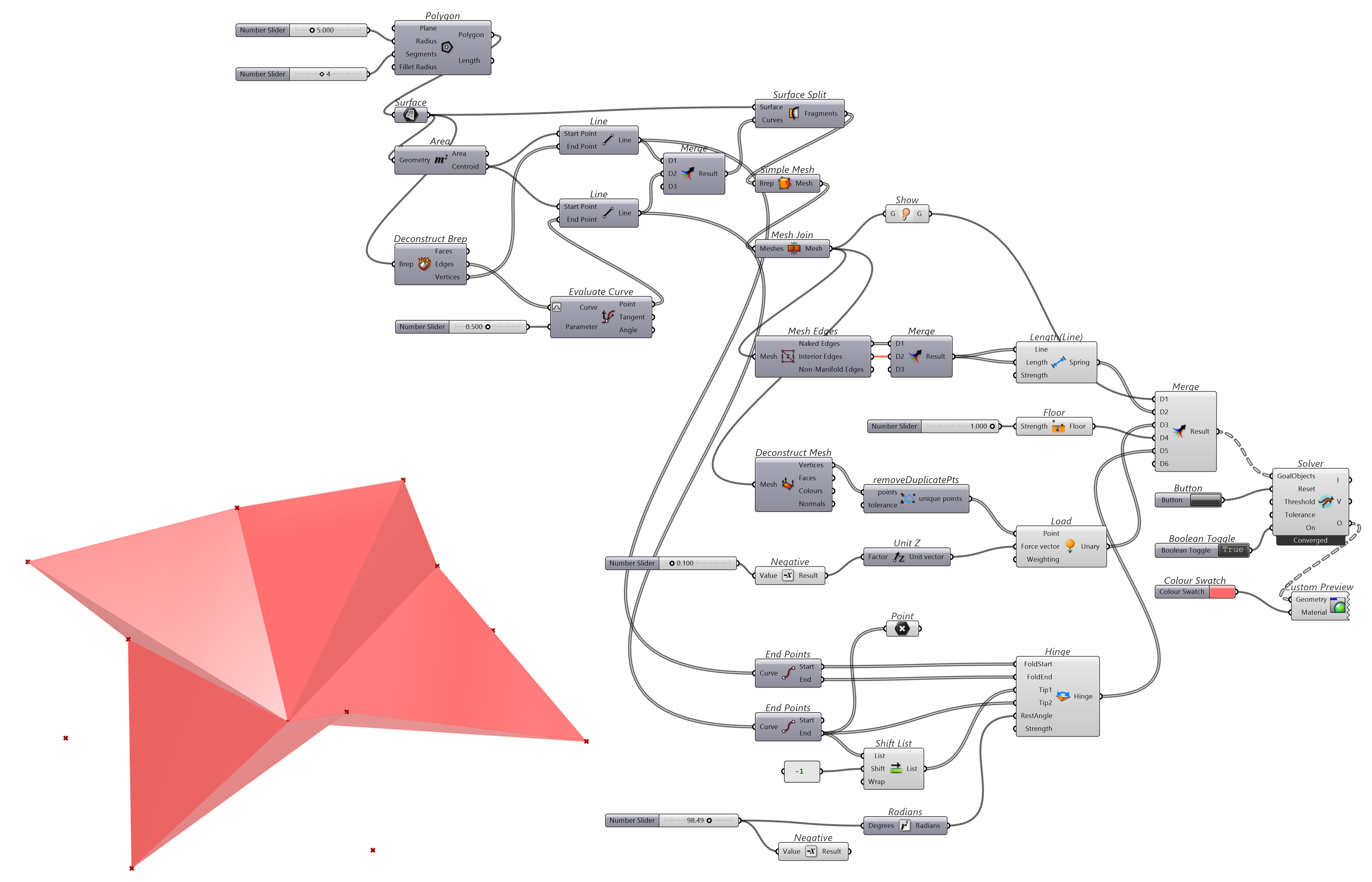
图 1.3.3-16 代码段（Kangaroo）-15与结果
⇩代码下载（codeSnippet_kangaroo_15.gh）
注释（Notes）：
① Weaverbird，是一个拓扑建模器，包含许多已知的网格细分算法和变换操作符（https://www.giuliopiacentino.com/weaverbird/）。