1.3.3 空间几何
Created on Tue Mar 22 15:57:42 2022; Last updated on Wed Aug 28 07:34:32 2024 @author: Richie Bao
点、线,面是几何学里的基本概念,是空间几何的基本要素。通常由点成线,由线成面,由面成体,由体围合空间,构成设计的具体内容。面在 GH 下有两类,一类是Surface;另一类是Mesh。不管是线,还是面,具体功用分类时,通常都含三类,一是,构建的方法。均包括于Primitive面板,为构建线面的基本几何对象。线中增加有Spline面板,即样条曲线(Spline Curve),由一组控制点得到一条曲线的方法及其扩展。在Surface中增加有Freedom面板,即自由曲面。在Mesh中增加有Triangulation面板,即三角网格;二是,线面的属性。为Analysis面板,通常包括提取或分解构成线面的基本对象,线面上一点的属性,例如该点上的切线、切面、或水平和垂直面等,及线面各自拥有的一些特性,例如线的区间、长度、提取点所具有的位置参数,Surface 的面积、体积、UV 坐标等,Mesh 单元面的法向量、边缘线等;三是,操作线面的工具。为Util面板,是对线面执行延长、裁切、偏移、倒角、打断、合并、反转方向、投影等操作,曲线(Curve)、曲面(Surface)和Mesh(格网)具体操作方法各有不同。
对于面,是使用 Surface 还是 Mesh,通常根据具体设计的内容确定,通常用 Surface 成体,但用 Mesh 处理类似建筑表皮具有单元面的几何对象。Mesh 由点的组织构建三角面Triangle或者四边面Quad,进而形成格网,会涉及更多数据组织的内容。
该章节将会自定义较多的封装组件,并组织和应用到代码逻辑中。这些封装组件除了基本常用的数据组织方法外,也在探索一些设计方法的构建逻辑,这类似于空间定位-点、向量与参考平面中的辅助地形设计-磁场、地形生成-磁场等,例如磁场影响自由变换曲面、盒体随机点磁场、曲面点线控制变换、曲面点线控制变换-力大小等;及特定设计内容的封装组件,例如梭柱、分形树生成(Python Script)、道路面构建-简、米仓-压顶、洞口-改-周期、米仓屋顶、吧台-A、幕墙-随机变化三边面、幕墙支撑-A、置石-A等;同时也包括盒体展平的flattenbox(Python Script),Mesh 对象展平的展平Mesh(Python Script)等工具。
1.3.3.1 曲线(Curve)
曲线部分代码段练习设计内容的想法来源于Giuliano Mauri①。Giuliano 设计和建造有大量自然枝杈编织的作品(图 1.3.3-1),充满自然、质朴的味道。而参数化设计的方法则可以充分发挥构建大量具有某一模式而又自然随机的形态。
Giuliano was born in Lodi Vecchio in 1938.At the age of 10, he worked as a baker 's assistant and painted billboards for the local cinema. In 1951 he moved to Milan. Here he works in a bakery and begins his career as a boxer in the “amateurs” championship, in the Welter weights, in the Lombard sports union. In 1959 he married Silvana and moved to Lodi, where, after the wedding, he opened a fresh pasta workshop. He continues to paint. From 1964 he frequented the artistic circles of Milan, in particular those linked to the Italian movement of militant poetry, which directed their attention towards the political and social environment.

图 1.3.3-1 Giuliano Mauri 设计作品
🍋🟩代码段-练习-1: ( )
图 1.3.3-2 中将梭柱部分构建的逻辑单独提取出来封装为组件梭柱(图 1.3.3-3_1),通过调整梭柱高度、截面圆半径获得不同的形态用于概念设计中建筑体核心筒和自然随意编织分离的表皮对象。
梭柱封装组件的输出端截面圆只包括顶底和中部的3个圆,需要增加更多的水平圆结构来支撑分离的外表皮对象,因此通过重新划分3个圆提取点连接的曲线,重新建立截面圆,构建重分截面曲线封装组件(图 1.3.3-3_2)。外表皮概念设计的代码建构逻辑是通过封装的可控随机间隔(1.3.1 代码段36)提取多个曲线上可控制等分间隔区间的随机点,避免纵向直线连接时互相碰撞交织。也应用了分枝-项值-random封装组件(1.3.1 代码段 34)生成 Tree 型随机数据,用于纵向直线随机延长,构造趋于自然随机的格栅。
这个概念设计会因为尺度的变化成为不同的设计对象,例如案例尺度下的观景台(或其它类型建筑概念原型);调小尺度及截面圆的变化,可以作为灯具造型等。

图 1.3.3-2 图 代码段(曲线)-1与结果
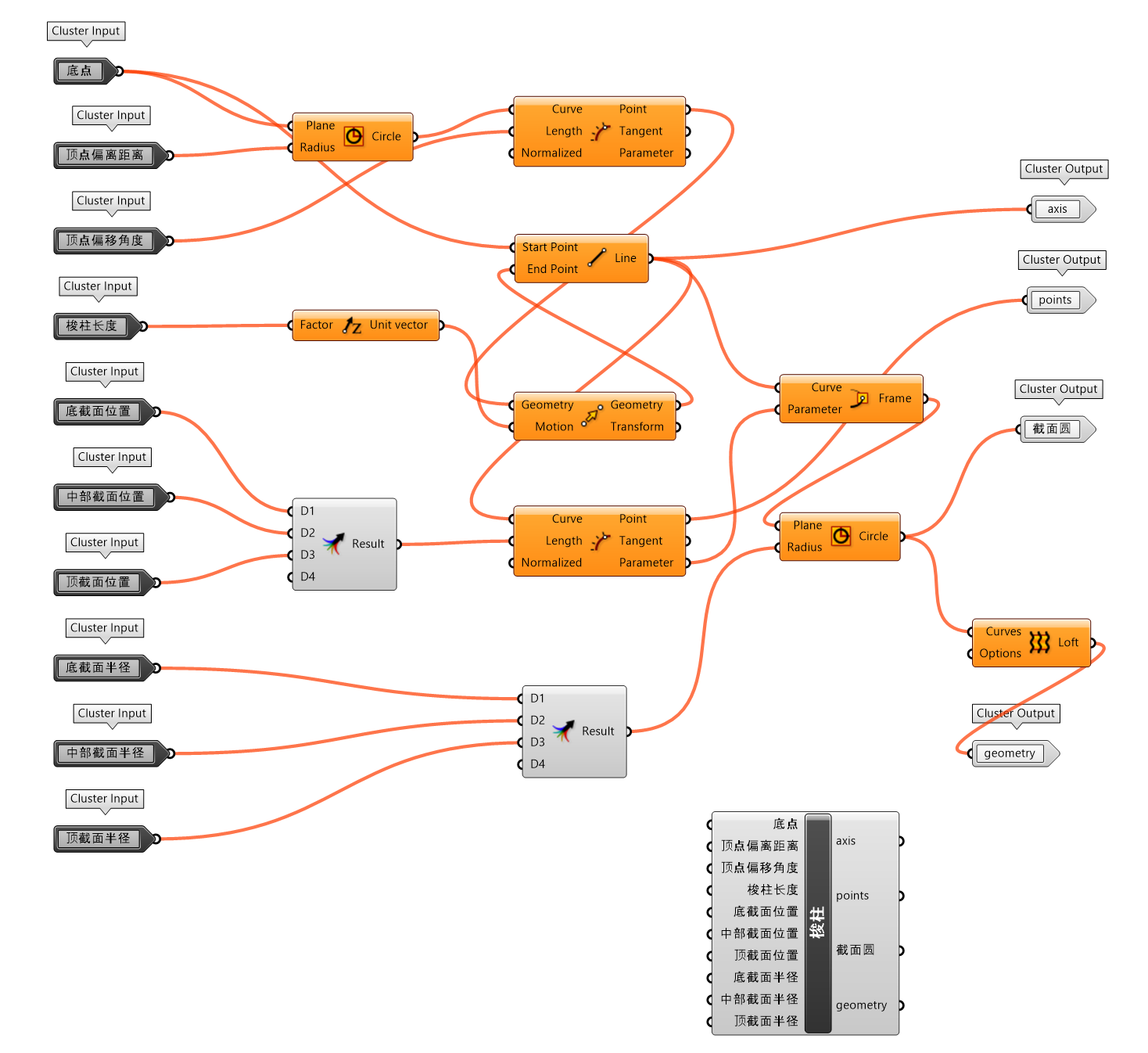
图 1.3.3-3_1 梭柱 封装组件 |
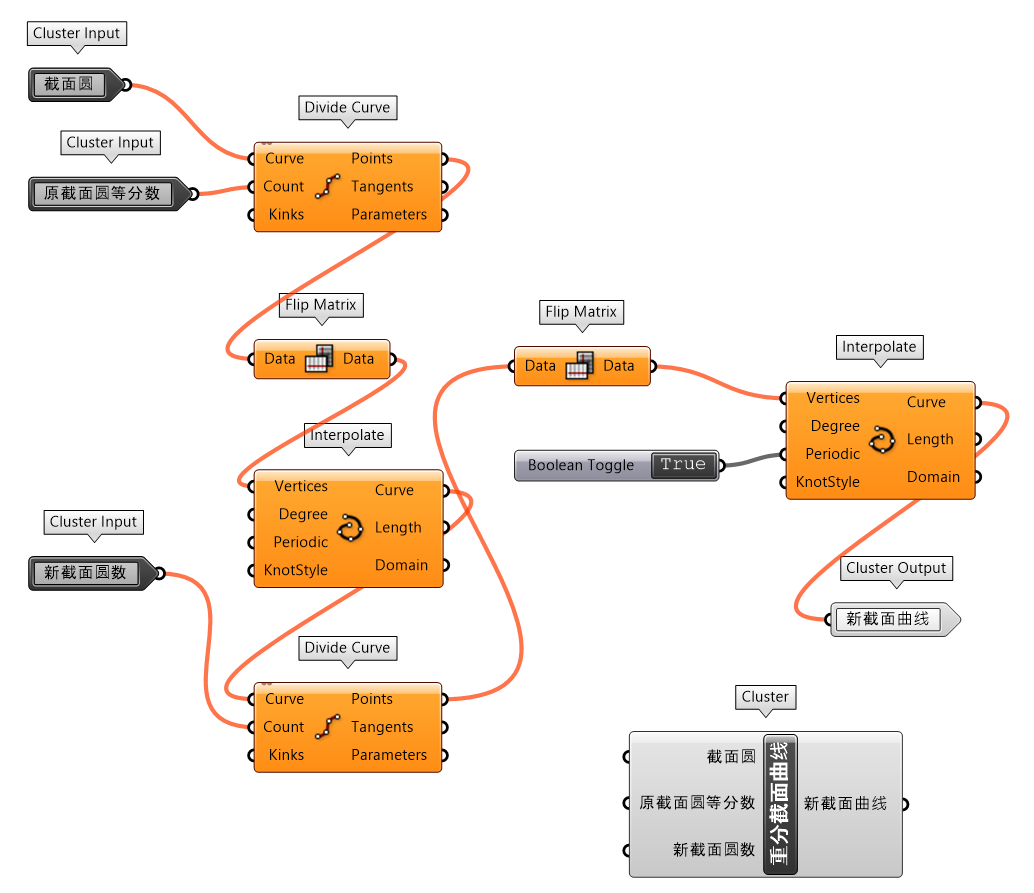
图 1.3.3-3_2 重分截面曲线 封装组件 |
图 1.3.3-4 代码段(曲线)-1
⇩代码下载(codeSnippet_geometry_01.gh)
🍋🟩代码段-练习-2: ( )
练习1中构建分离的外表皮格栅对象时,是对水平圆两两分组建立多层纵向直线。图 1.3.3-5里构建的水平向自然随机编织的棚架同样需要对支撑结构两两分组,并在水平向上连接为直线段,因此将练习1中该部分代码提取出来,单独封装为两两分组随机延长直线(图 1.3.3-6_1),方便用于类似设计的使用。注意到构建支撑结构的方法,一是,用图形函数Graph Mapper组件调出具有韵律渐变的圆大小;二是,配合用Seam和Sub Curve组件提取部分圆;三是,通过对各个截面圆双侧偏移后建立的缓冲区域Populate Geometry多个随机点,建立具有随机自然形态的支撑结构线。同时调整了已封装的人参考定位(1.3.1 代码段37)为人参考定位-方向(图 1.3.3-6_2 ),可以通过旋转控制人的朝向。
设计上尽量保持水平向编织的延申感,因此在后续深化设计上,如何确保支撑结构的设计不打破水平延申意象或尽量弱化纵向切割感,会成为设计的一个重点和难点。最后的代码如图 1.3.3-7。

图 1.3.3-5 代码段(曲线)-2的结果:动画

图 1.3.3-5 代码段(曲线)-2的结果
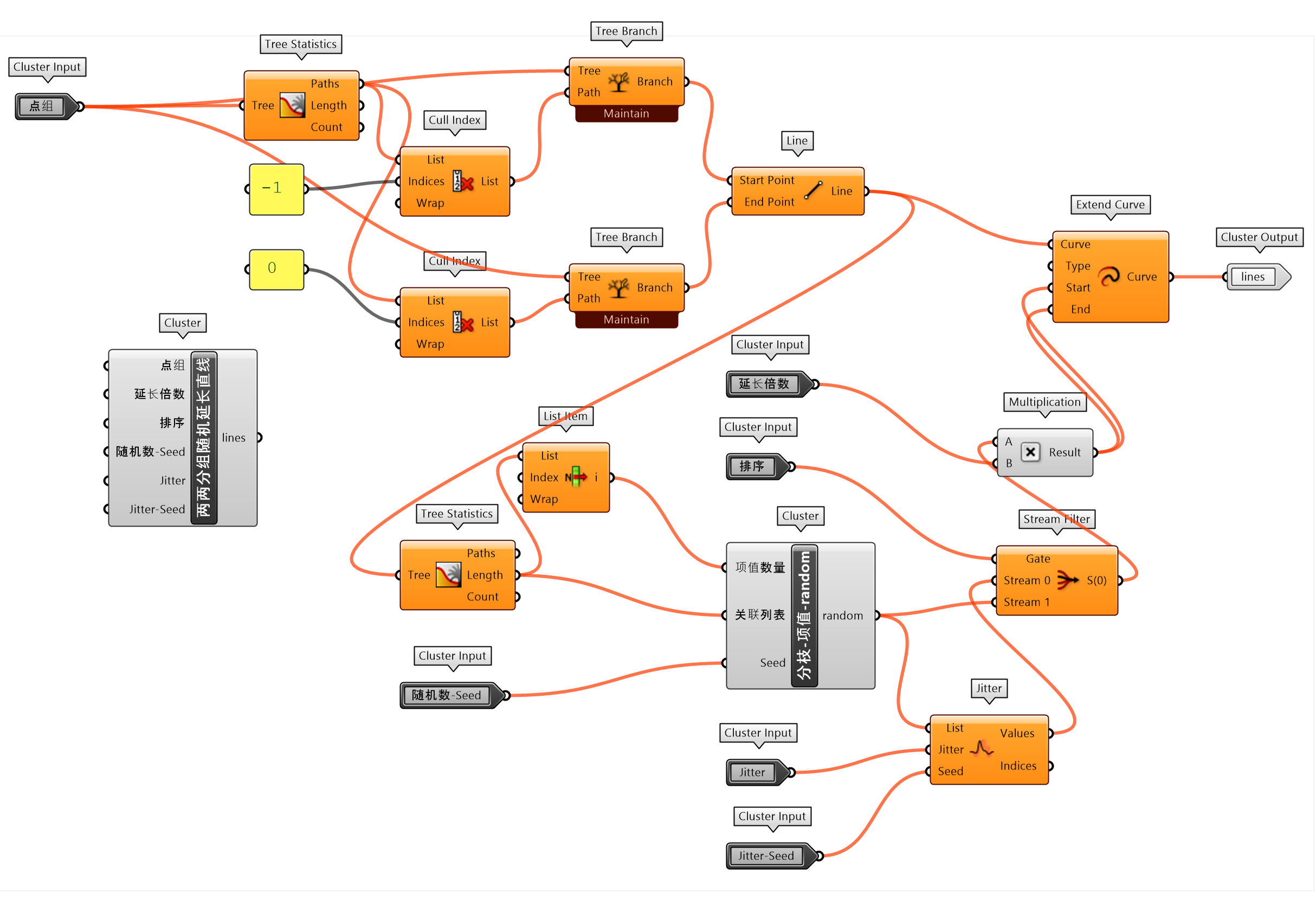
图 1.3.3-6_1 两两分组随机延长直线 封装组件 |
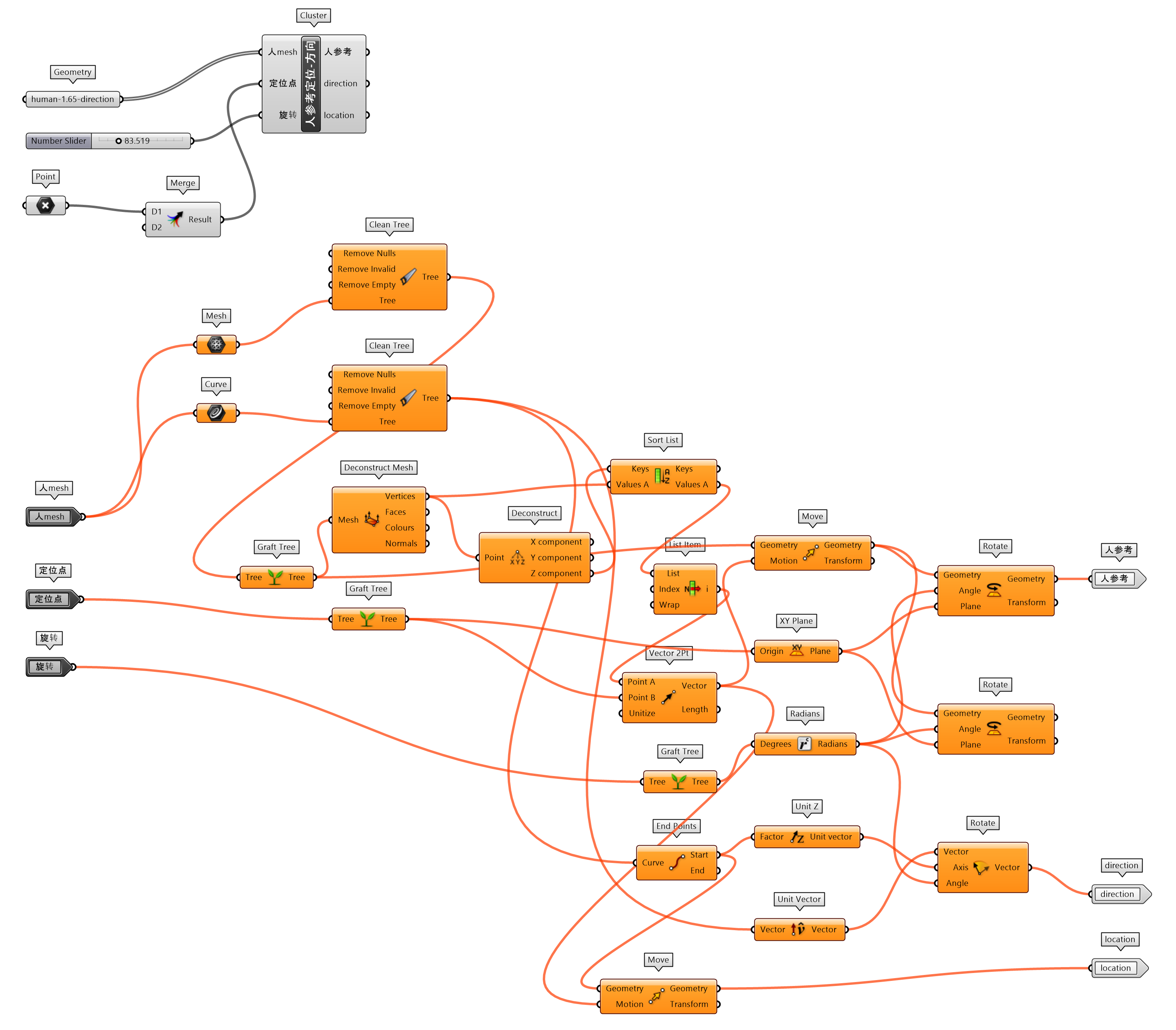
图 1.3.3-6_2 人参考定位-方向 封装组件 |
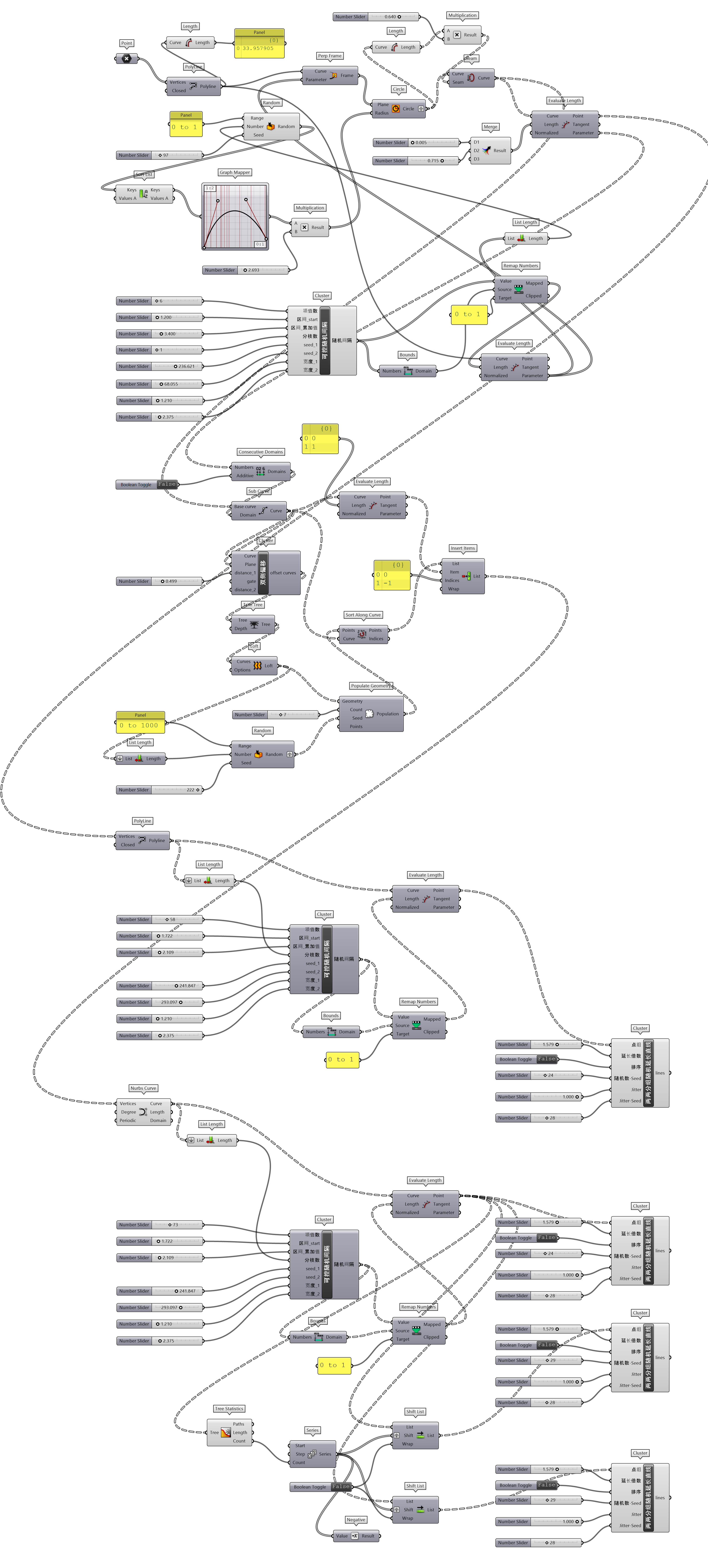
图 1.3.3-7 代码段(曲线)-2
⇩代码下载(codeSnippet_geometry_02.gh)
🍋🟩代码段-练习-3: ( )
向日葵形态的概念设计虽然与练习1、2不同,但是可以看到核心的构建逻辑保持一致。用可控随机间隔提取区间可控避免纵向直线连接碰撞的随机点对象;及由双侧偏移曲线构建面后,由Populate Geometry生成随机点,用于连接为新自由变化的曲线或折线。

图 1.3.3-8 代码段(曲线)-3 结果动画

图 1.3.3-8 代码段(曲线)-3和结果
⇩代码下载(codeSnippet_geometry_03.gh)
🍋🟩代码段-练习-4: ( )
图 1.3.3-10 仍旧保持自然随机编织的设计形态(核心逻辑仍未发生改变),只是将其赋予于了变化的元球(MetaBall(t) Custom)水平结构线之上。
练习2中两两分组随机延长直线是垂直向支撑结构直线的随机延长,这里则是依附于元球水平结构线上的设计,不是垂直于支撑结构线的变化,因此调整内部代码,封装为两两分组随机延长直线_not flip组件(图 1.3.3-10)。实际上,最好的处理方法是在两两分组随机延长直线中增加输入端项,可以选择变化是否翻转。
GH->Mesh->Triangulation下提供有MetaBall、MetaBall(t)和MetaBall(t) Custom3种构建元球的途径。点之间的不同距离、阈值的控制可以融合或分离单个元球和融合时的结合度,这有助于寻找适合的结合形态。三维元球的获取是用多个参考平面(输入端Plane)切割提取,元球自然韵律变化的大小配合使用Range和Graph Mapper组件生成的连续变化数值构建。

图 1.3.3-9 代码段(曲线)-4的结果:动画
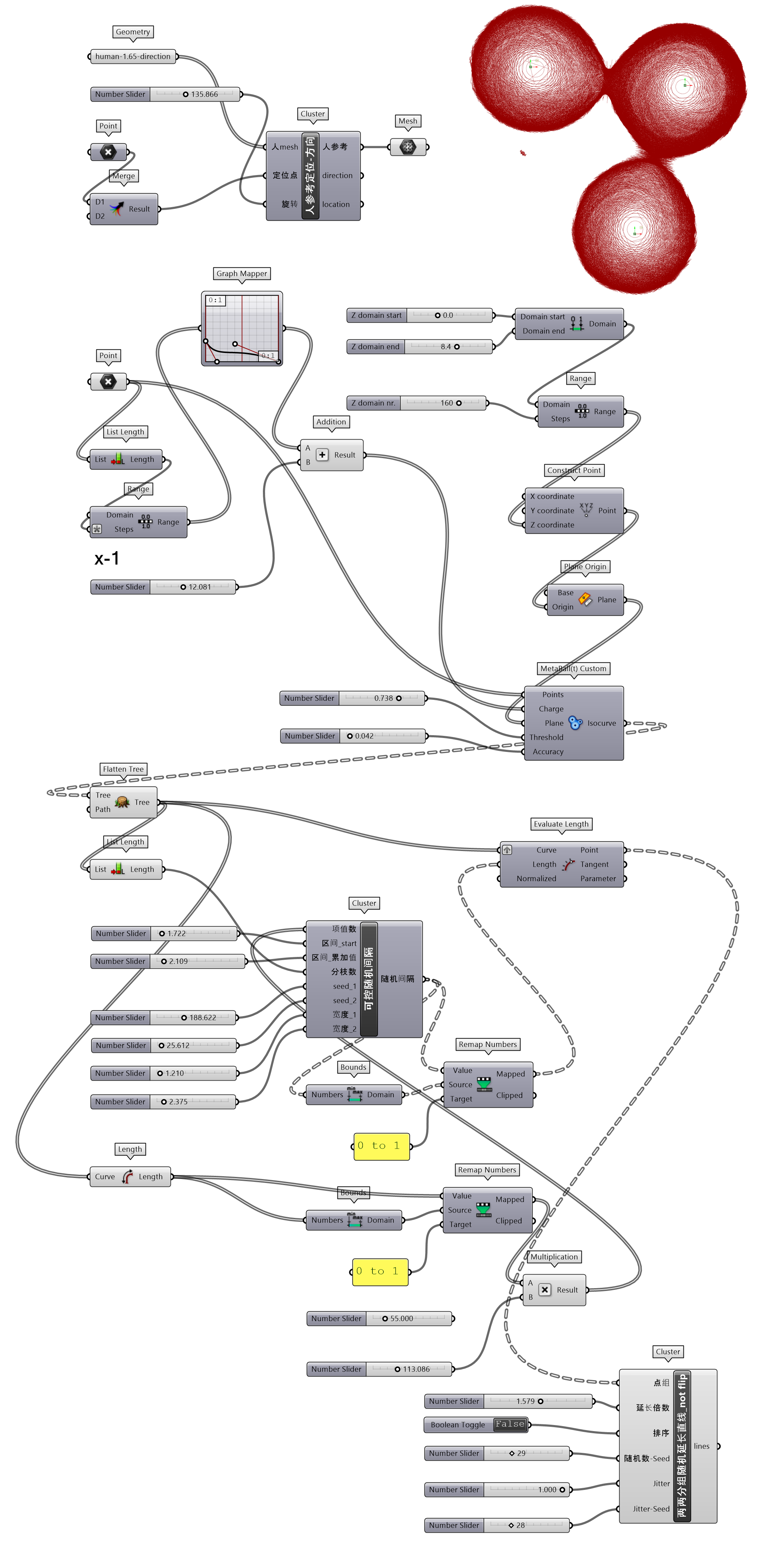
图 1.3.3-9 代码段(曲线)-4和结果
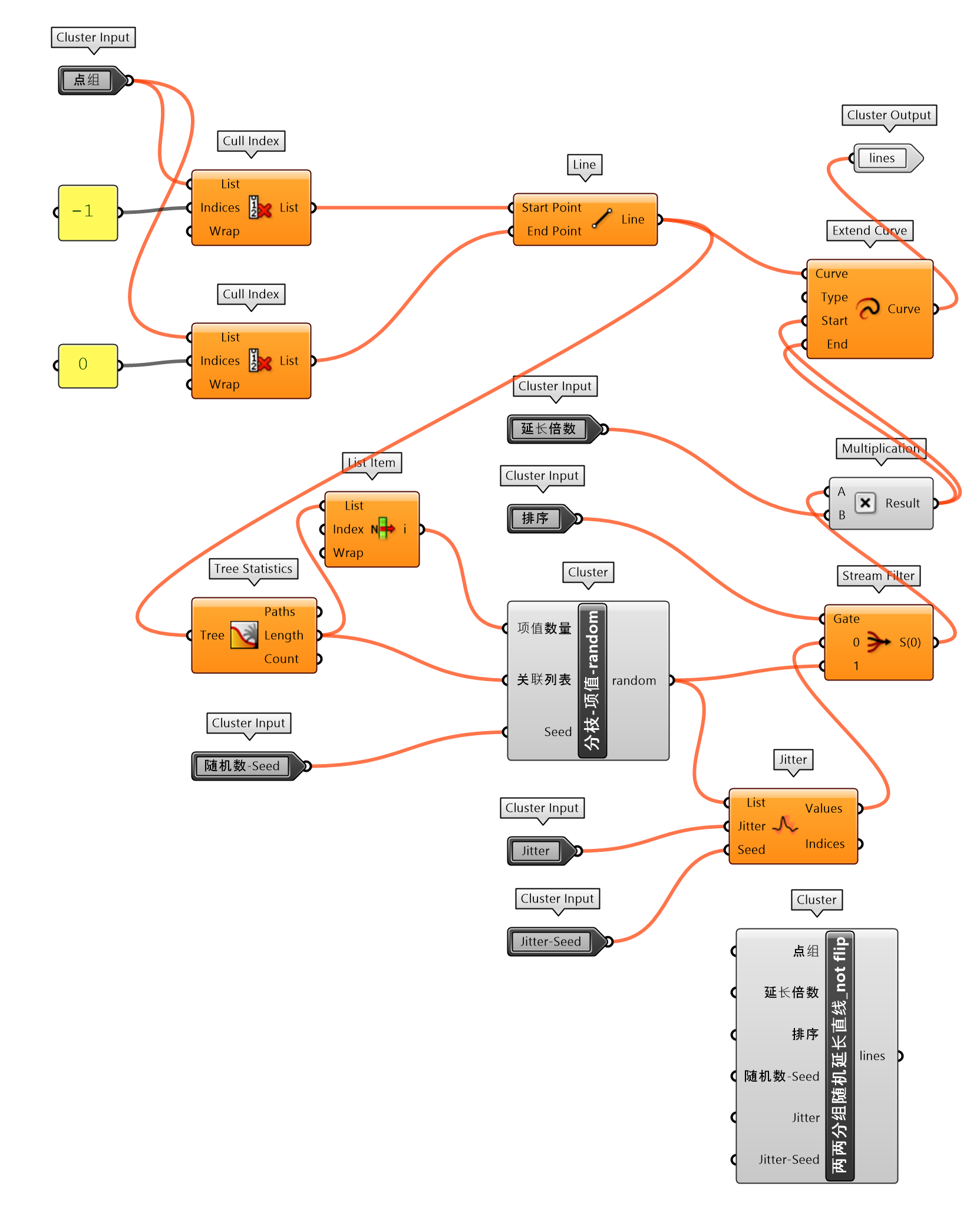
图 1.3.3-10 两两分组随机延长直线_not flip 封装组件
⇩代码下载(codeSnippet_geometry_04.gh)
🍋🟩代码段-练习-5: ( )
图 1.3.3-11 为给定任何形式的设计边界,建立对分2直线(图 1.3.3-12)的方法,设计可控交织程度的条带行铺地形式。通过提取设计边界随机多个点,Shift List组件可以偏移这些点的索引值,进而控制Split List组件切分这些点为两组点的位置。两组已经按设计边界排序的点,可以通过Jitter组件输入端Jitter控制随机大小来控制交织程度。
这一设计逻辑除了用于铺地形式之外,练习中也将这一逻辑赋予到Voronoi Cell组件建立随机泰森多边形单元表皮,围合出一个闭合的空间,作为镂空的木屋、棚架等设计内容的概念原型。

图 1.3.3-11 代码段(曲线)-5的结果:动画

图 1.3.3-11 代码段(曲线)-5的结果
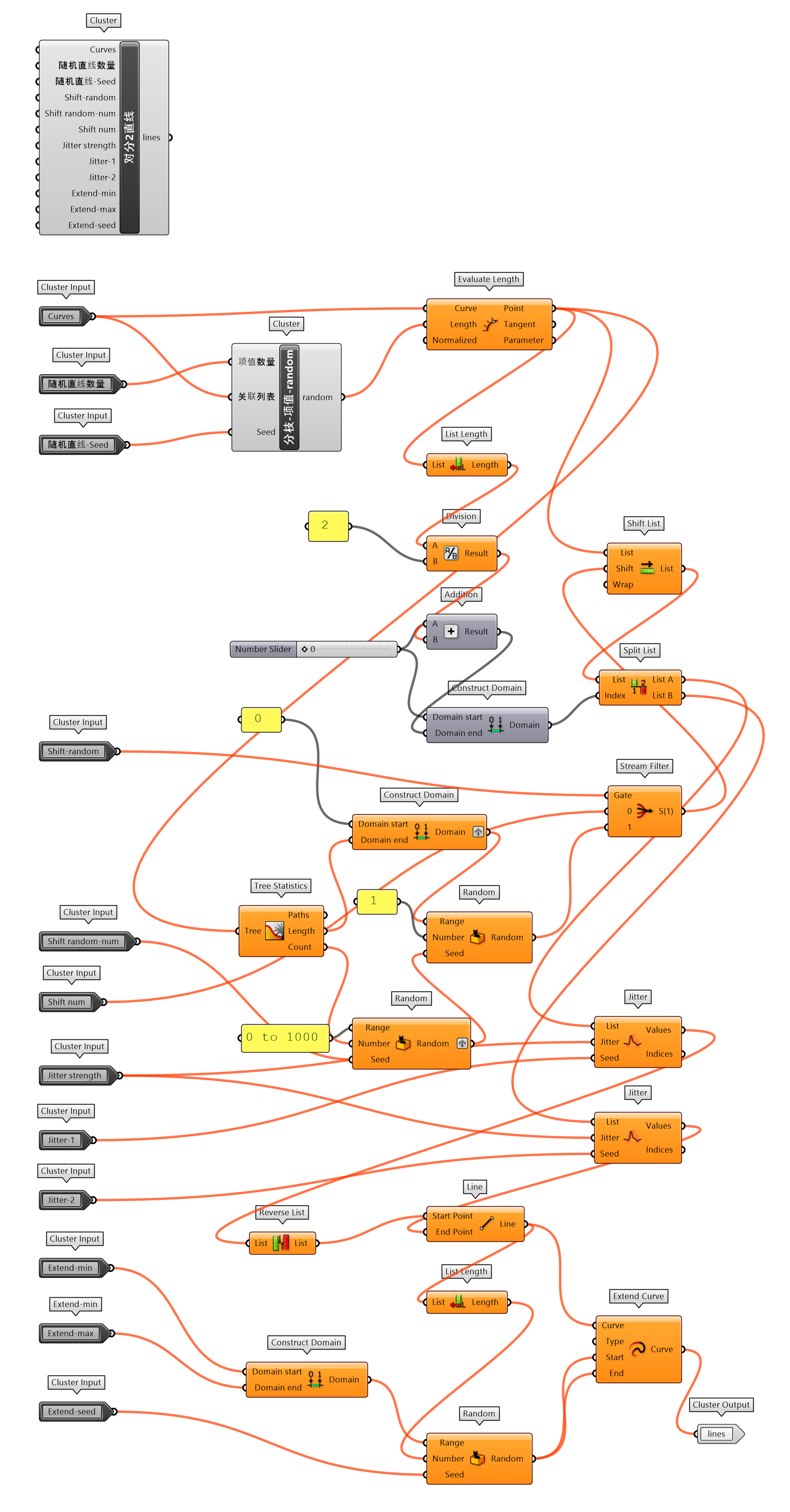
图 1.3.3-12 对分2直线 封装组件
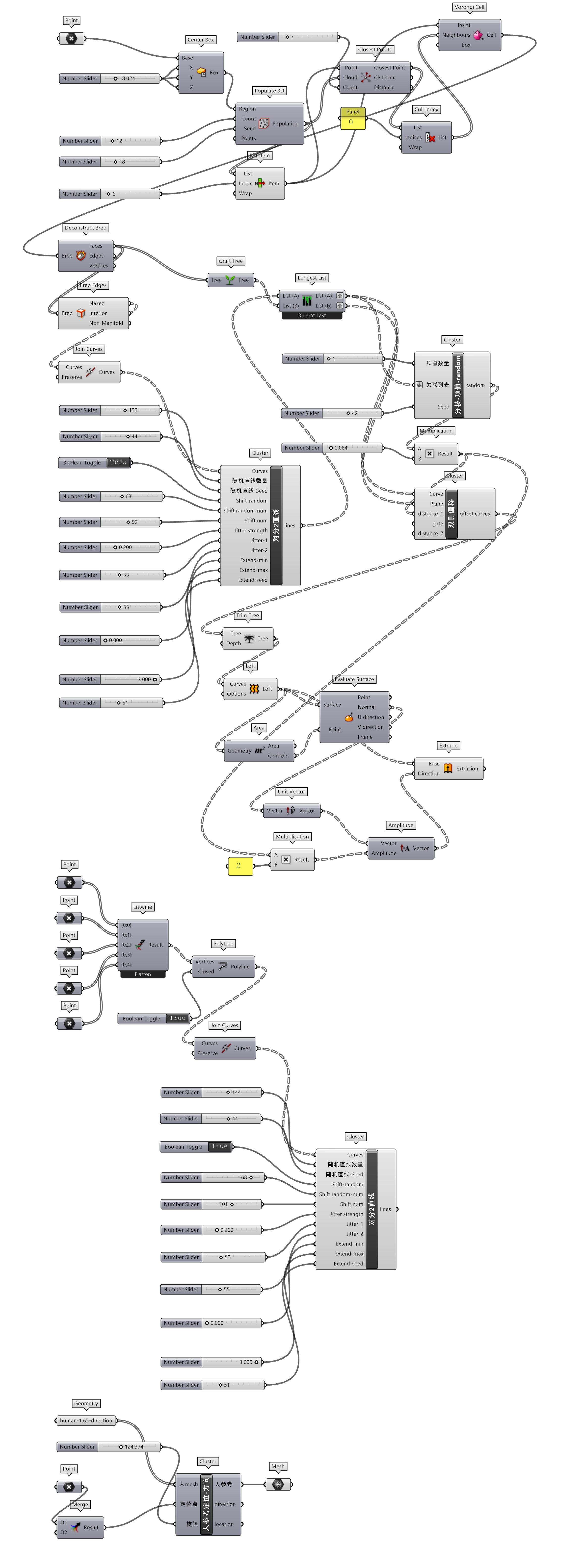
图 1.3.3-13 代码段(曲线)-5
⇩代码下载(codeSnippet_geometry_05.gh)
🍋🟩代码段-练习-6: ( )
图 1.3.3-14 设计概念源于树木枝丫,于是给出了一个三维树和一个平面树形态。三维树的 Python 代码更新于 Pavlo Menshykh 的Procedural vegetation for BIM②fractal tree generator。平面树形态则首先构建多个渐变的同心圆,提取各圆上的随机点后,两两一组由外层点各点向内层点寻找最近点连为枝丫,并封装为树-平面分支组件(图 1.3.3-15)。平面树的构建逻辑可以拓展到非圆的形态,例如多个水平向空间变化曲线之间的枝丫形态,及类似非平面的空间曲线等。

图 1.3.3-14 代码段(曲线)-6和结果:动画
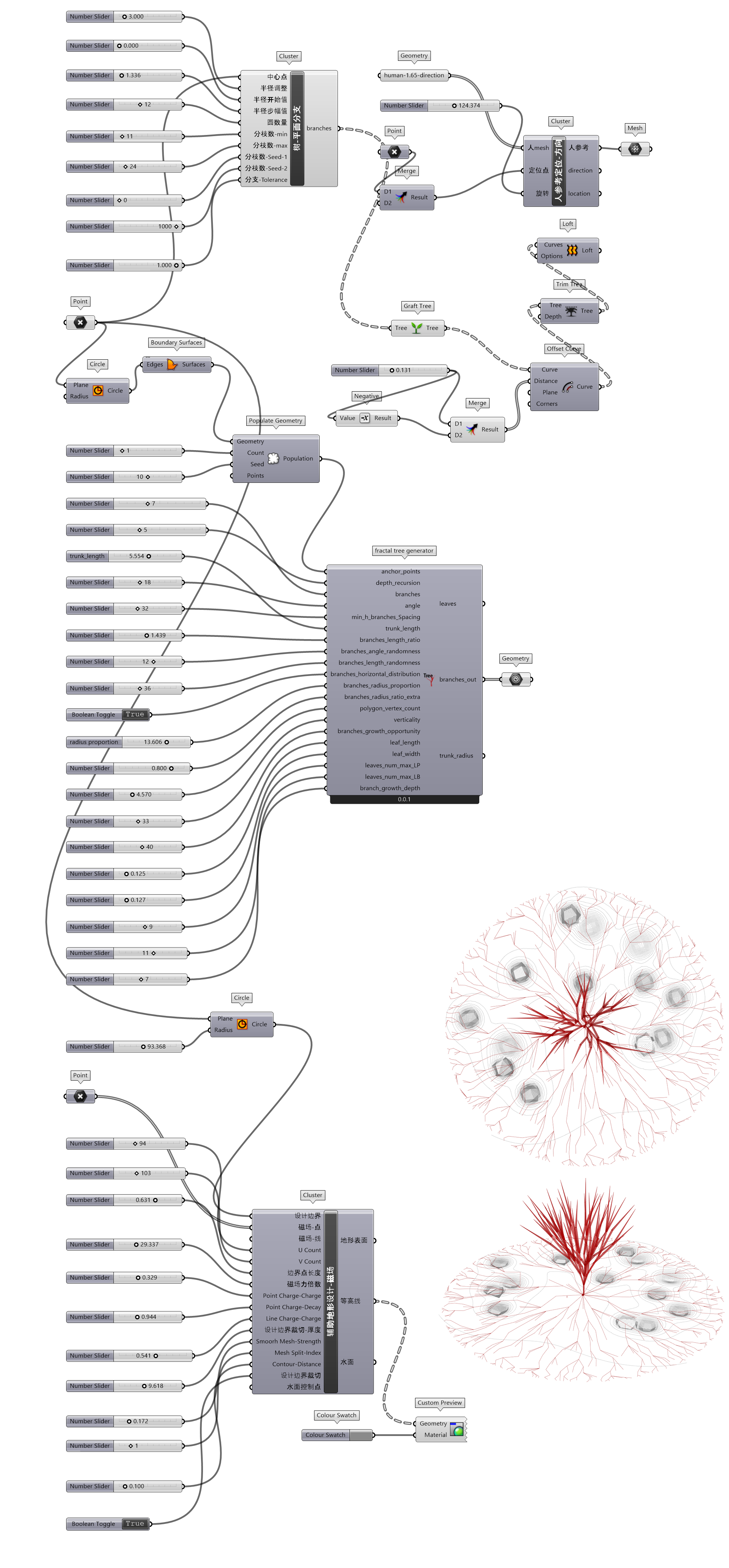
图 1.3.3-14 代码段(曲线)-6和结果
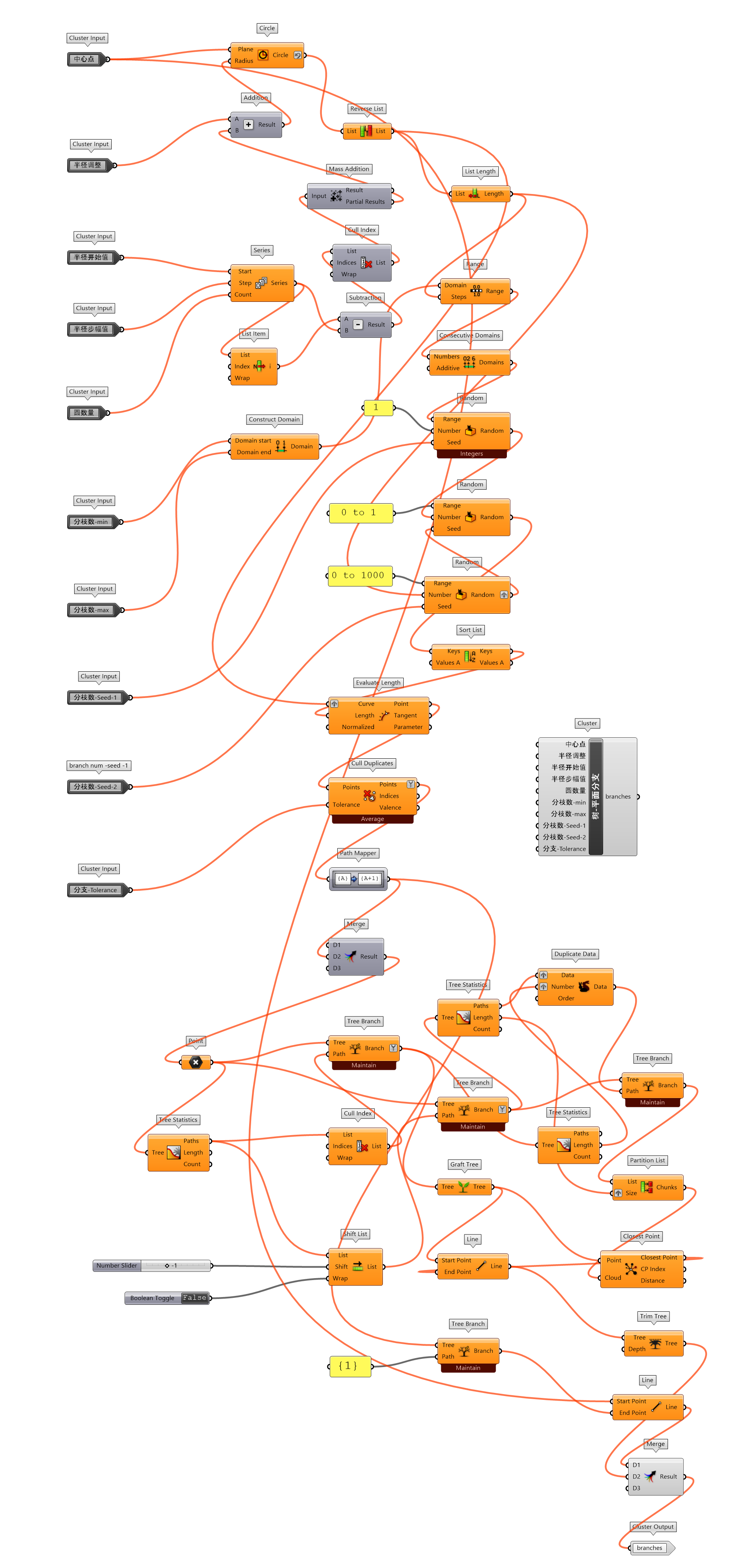
图 1.3.3-15 树-平面分支 封装组件
fractal tree generator(Python Script 组件)源码可以查看下载文件,或者从原作者 GitHub 仓库Procedural-vegetation②中获取。
⇩代码下载(codeSnippet_geometry_06.gh)
🍋🟩代码段-练习-7: ( )
同练习1、2、4、5的基本构建逻辑,图 1.3.3-16将这一逻辑应用到一个旋转的弧上,通过开合的程度和位置,构建棚架或屋宇的雏形。

图 1.3.3-16 代码段(曲线)-7和结果:动画

图 1.3.3-16 代码段(曲线)-7和结果
⇩代码下载(codeSnippet_geometry_07.gh)
🍋🟩代码段-练习-8 ( )
曲线部分的代码段练习通常由可控随机间隔、两两分组随机延长直线或两两分组随机延长直线_not flip建立垂直或者水平于给定结构线、随机变化的枝丫状格栅。当不把这枝丫格栅作为表皮层处理,而类似图 1.3.3-17的练习,具有很大厚度或者进深的多层格栅时,试图影射一种穿越茂密丛林般的感受。
设计中经常要提取垂直于给定直线或曲线的垂直线,因此将这一构建逻辑封装为垂直曲线的线段组件(图 1.3.3-18),以便调用。最终代码为图 1.3.3-19。

图 1.3.3-17 代码段(曲线)-8的结果:动画

图 1.3.3-17 代码段(曲线)-8的结果
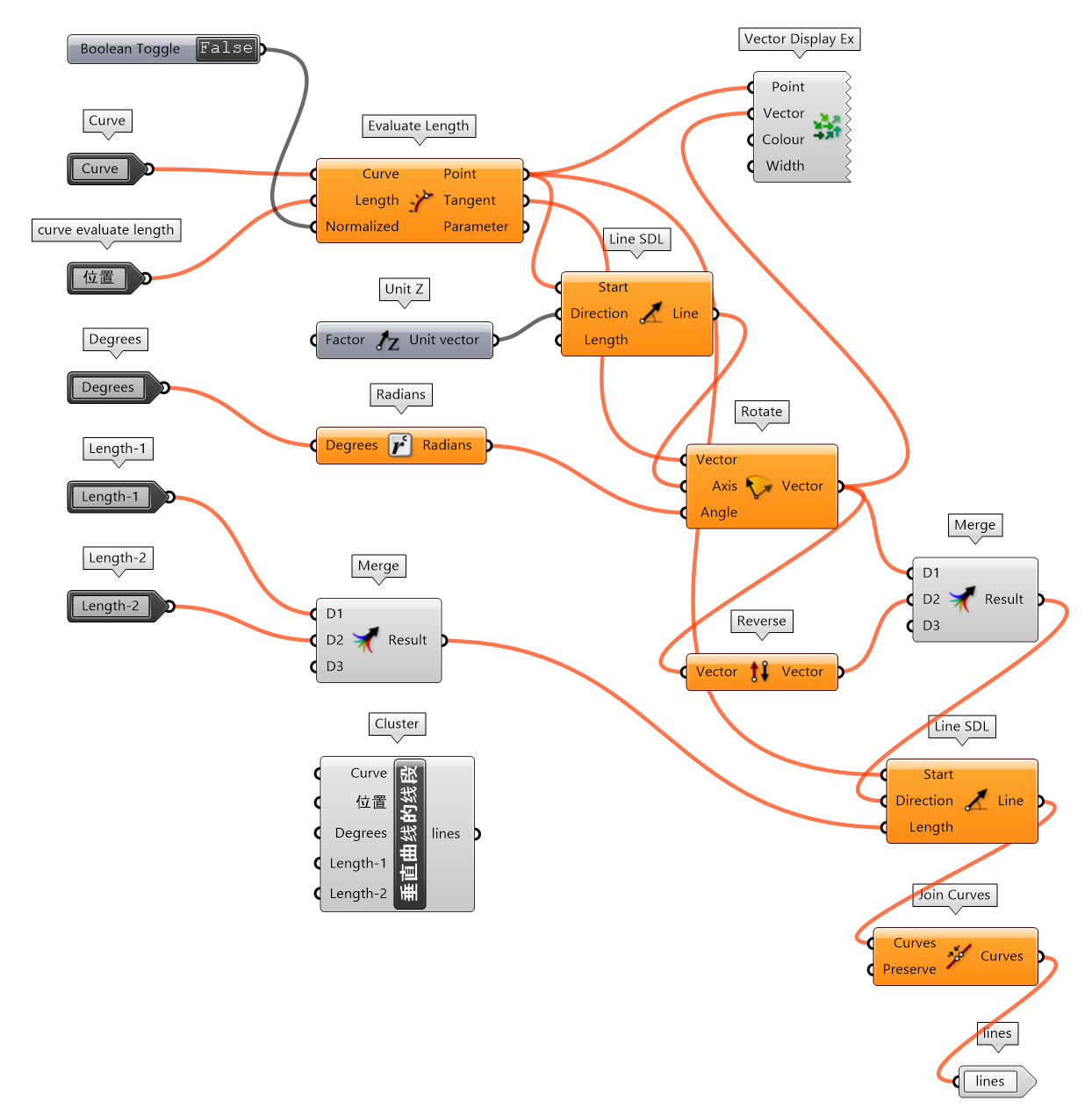
图 1.3.3-18 垂直曲线的线段 封装组件
图 1.3.3-19 代码段(曲线)-9
⇩代码下载(codeSnippet_geometry_08.gh)
🍋🟩代码段-练习-9 ( )
限定空间的一种简单方法是在这潜在空间区域一角给定一个对象,从而在心理上暗示性的勾勒出这一空间。曲线部分的最后一个代码段练习,是基于练习8,在屋前侧给了一个由对分2直线封装组件堆叠的立方体构筑,内部可以藏灯,当灯火从这些枝丫中散漫透出时,期待表达出林中木屋灯火丝丝的暖意。

图 1.3.3-20 代码段(曲线)-9的结果:动画

图 1.3.3-20 代码段(曲线)-9的结果
图 1.3.3-21 代码段(曲线)-9
⇩代码下载(codeSnippet_geometry_09.gh)
1.3.3.2 曲面(Surface)
空间以体围合,因此体往往是设计的对象,但是有些对象在设计时通常以面的形式对待,例如地形表面,建筑表皮等。因此对于 Surface 的学习可以从构建体对象和构建面对象出发。对于体,大部分代码段练习案例基本都有包含,因为点线除了用于分析、作为概念的结构线,基本上都是作为构建面的基本元素,而面成体后成为实际设计建造的对象,这也基本是最终设计的表达,例如木构造部分的房屋构件等;对于面,相对现实对象而言,是厚度趋于零,约为面的体,当然这往往只是在设计概念上的表述,当深化设计时,面要归为体,成为现实中要实际对应的对象。
设计代码段时,除了思考设计内容和形态外,通常会想,用哪种途径来辅助或者生成设计,如何构建设计的工具。辅助地形设计-磁场和地形生成-磁场就为构建的一种工具,可以辅助地形设计。那么对于曲面来讲,尤其构建自由变化的曲面时,什么样的工具可以有效辅助设计?
🍋🟩代码段-练习-10 ( )
磁场影响自由变化曲面(图 1.3.3-22)辅助设计工具的建构,是探索自由变化曲面构建的一种途径,将要处理的对象放置于一个给定的磁场域下,来影响域内对象控制点的空间位置,进而改变对象形态的变化。这一工具可以应用到任何具有可调控控制点的曲面对象上,只需要将磁域空间笼罩于该对象,该对象可以是建筑、构筑单体,也可以是场地区域。
图 1.3.3-23练习是变化建筑表皮的示例,如果是单一的金属板,在后续结构设计时,可能会以最简单方格网的形式将其划分为适合加工尺寸的多个嵌板,最后再拼接。如果希望突出嵌板之间的纹路,或者设计时就有意利用曲面 UV 曲线或者等值线作为设计纹路,则需要进一步考虑材料的选择,方便加工和建造。

图 1.3.3-23 代码段(曲面)-10的结果:动画
图 1.3.3-22 磁场影响自由变化曲面 封装组件
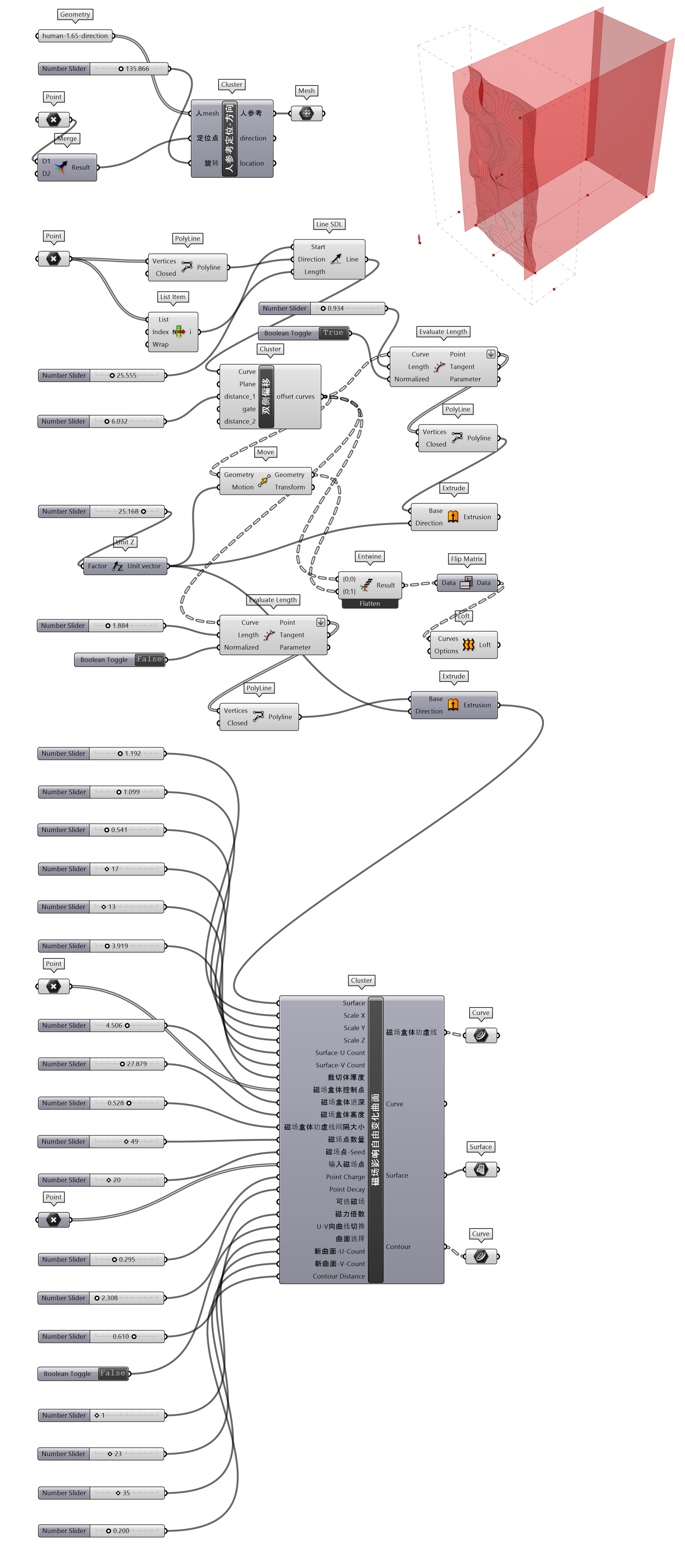
图 1.3.3-23 代码段(曲面)-10和结果
⇩代码下载(codeSnippet_geometry_10.gh)
🍋🟩代码段-练习-11 ( )
磁场影响自由变化曲面辅助设计工具,输入端参数Surface限制了工具使用的自由性,因此调整缩减该代码的输入条件,砍去了Surface及对其相关变换操作的输入端选项参数,调整为提取点输入参数,仅保留建立盒体磁域的代码部分,封装为盒体随机点磁场(图 1.3.3-24)。这样的调整可以将更具变动性输入对象的曲面点提取扩大为更多的形态。
图 1.3.3-25 将一个球体穿越过盒体随机点磁场的磁域空间,在磁域内磁力作用下,球体表面的点位置发生了变化,构建出受到拉伸或挤压的形态。

图 1.3.3-25 代码段(曲面)-11和结果:动画
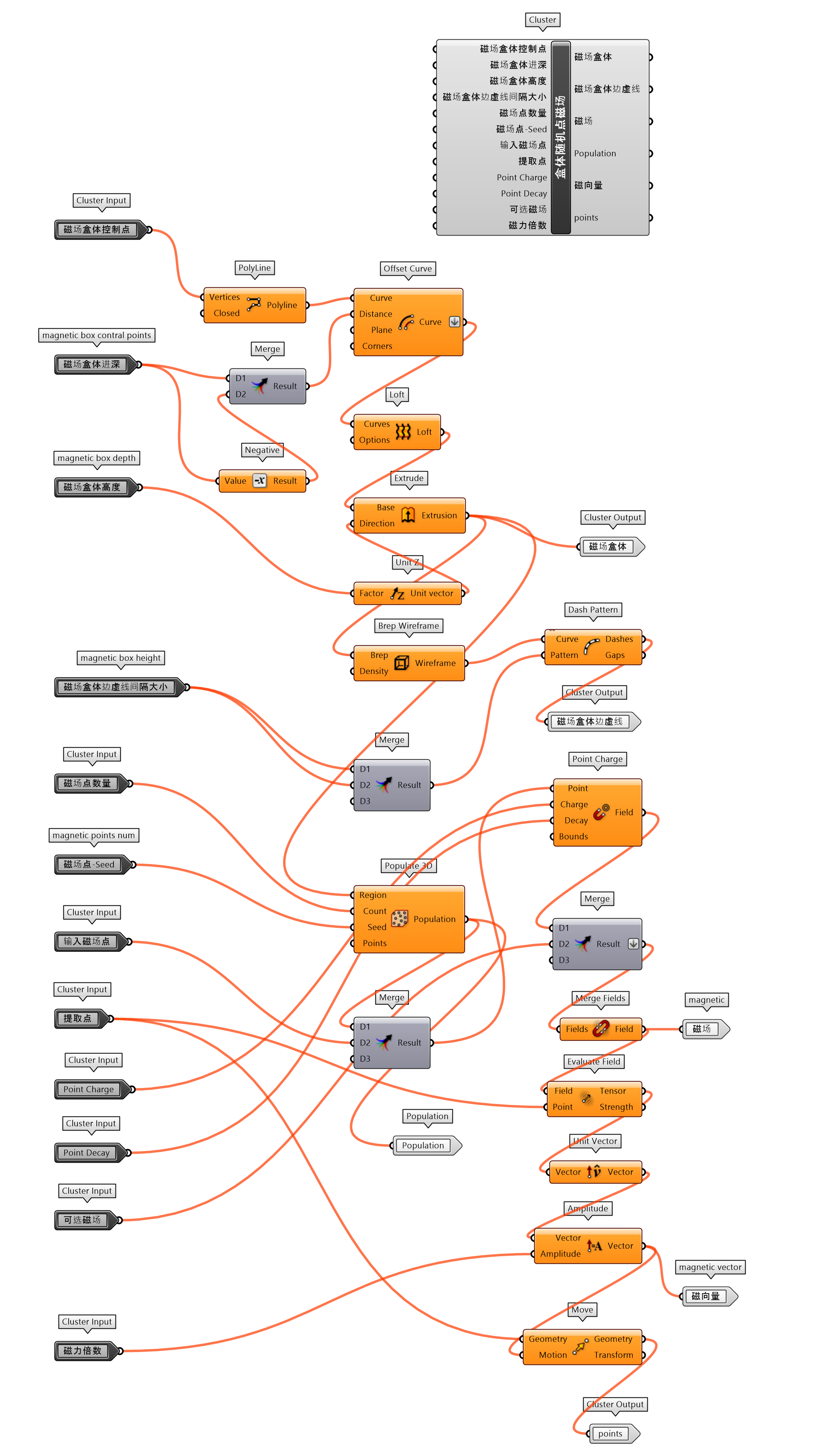
图 1.3.3-24 盒体随机点磁场 封装组件
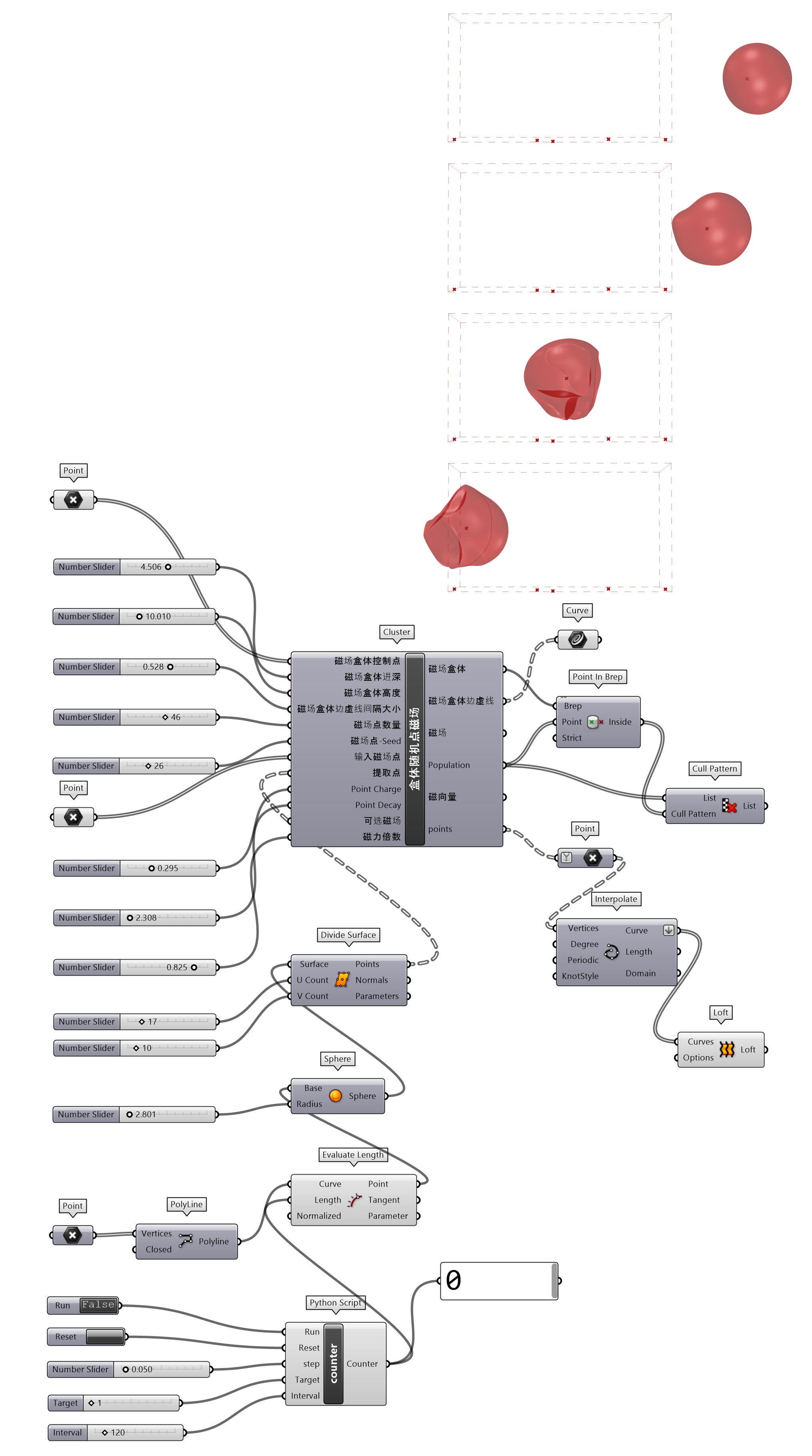
图 1.3.3-25 代码段(曲面)-11和结果
⇩代码下载(codeSnippet_geometry_11.gh)
🍋🟩代码段-练习-12 ( )
图 1.3.3-26是一个非常简单的逻辑形态,归功于Voronoi 3D和MultiPipe组件,能够直接构建出骨骼形态的空间异形网架。

图 1.3.3-26 代码段(曲面)-12和结果:动画
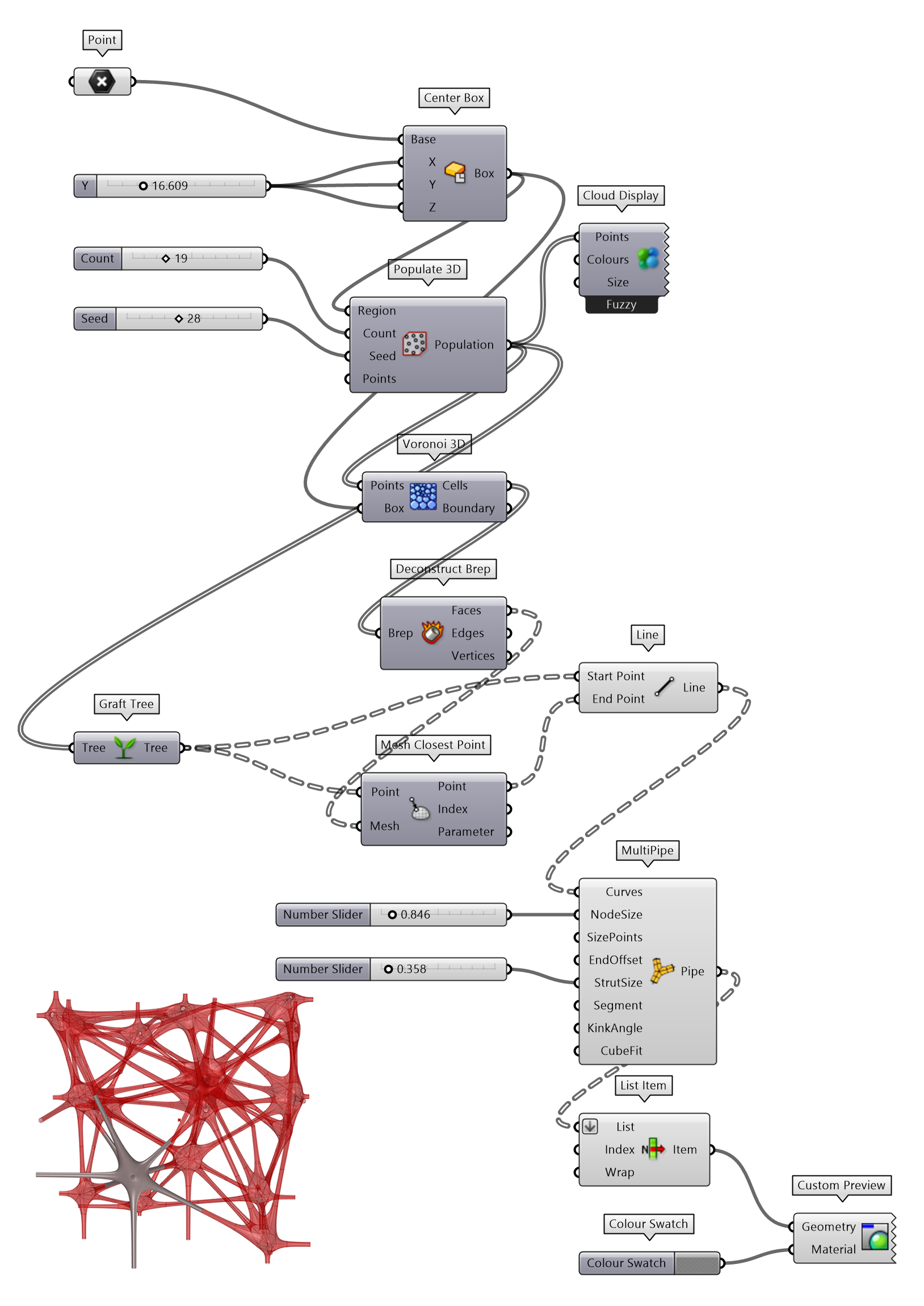
图 1.3.3-26 代码段(曲面)-12和结果
⇩代码下载(codeSnippet_geometry_12.gh)
🍋🟩代码段-练习-13 ( )
关于地形的设计工具,采用了自动生成和手工辅助调整两种策略,应对不同的使用场景。对于曲面的调整除了上述磁场影响自由变化曲面和盒体随机点磁场外,希望能够增加手动调整以更精准控制曲面变化的方式,因此构建了曲面点线控制变化的工具(图 1.3.3-27)。实际上,这个工具的构思源于“空间定位-点、向量与参考平面”部分练习4吸引子的构建逻辑。这里抽取出了其核心的算法,给出主要输入参数和需要输出的参数进行封装。通过控制曲线和控制点影响曲面的点曲面点组空间位置,输出新的位置点组Points。
为什么要通过吸引子来变化曲面,而不直接使用 RH 下手工调整曲线的方法?一是,因为一般构建的途径需要调整每一根曲线后,再由这些曲线连为曲面。对于有些设计内容来讲,这样处理的方法会异常笨拙,也不容易调整为理想中的空间形态。而吸引子的方法可以影响周边点(曲面)的变化,通过主要控制线的调整,就可以达到理想空间营造的目的(或者为纯粹的设计形式);二是,因为参数化意义本身,以构建参数可调的逻辑。那么,如果对吸引子(控制曲线和控制点)进一步编程使其也具有自动生成,或者优化的逻辑,曲面点线控制变化的工具也可以成为自动生成的工具,这是 RH 本身所不具有的,也是为什么未使用SubD Tools工具(类似于表面雕刻,可以手动变化曲面,同时影响周边曲面单元)的原因。
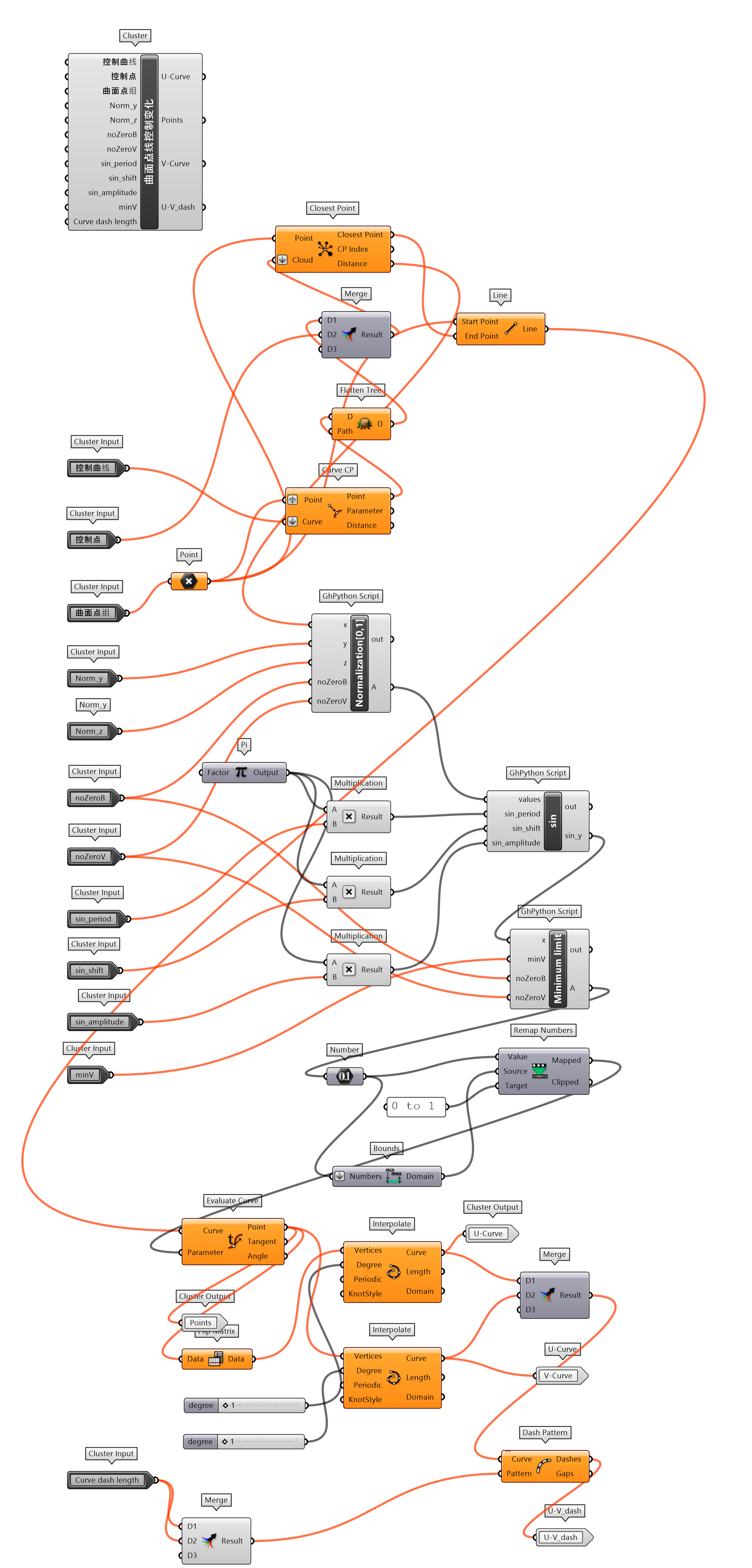
图 1.3.3-27 曲面点线控制变化 封装组件
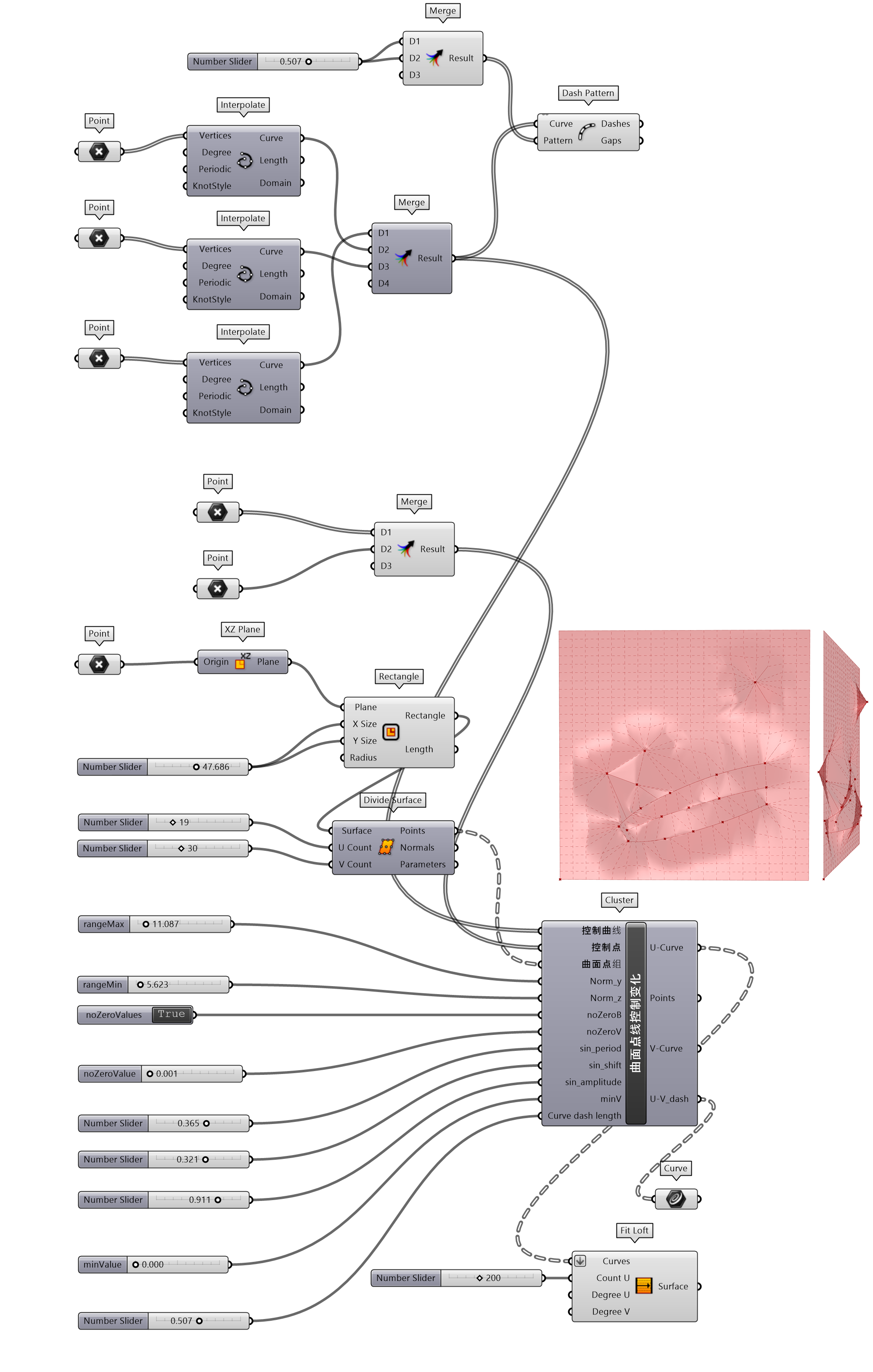
图 1.3.3-28 代码段(曲面)-13和结果
⇩代码下载(codeSnippet_geometry_13.gh)
🍋🟩代码段-练习-14 ( )
图 1.3.3-29为应用曲面点线控制变化工具的例子,在近似盒体建筑中的两面墙体上增加一体化的幕墙结构。需要注意,这里使用了LUNCHBOX③扩展组件下的Space Truss Structure 2方法,可以在给定的两个曲面间自动构建网架(空间桁架)结构线,避免重复造轮子,从而节约大量的时间和精力。在网架的细节设计上参考Lunchbox Grasshopper - Space Truss④方法,增加了连接件和紧固件的设计形式。
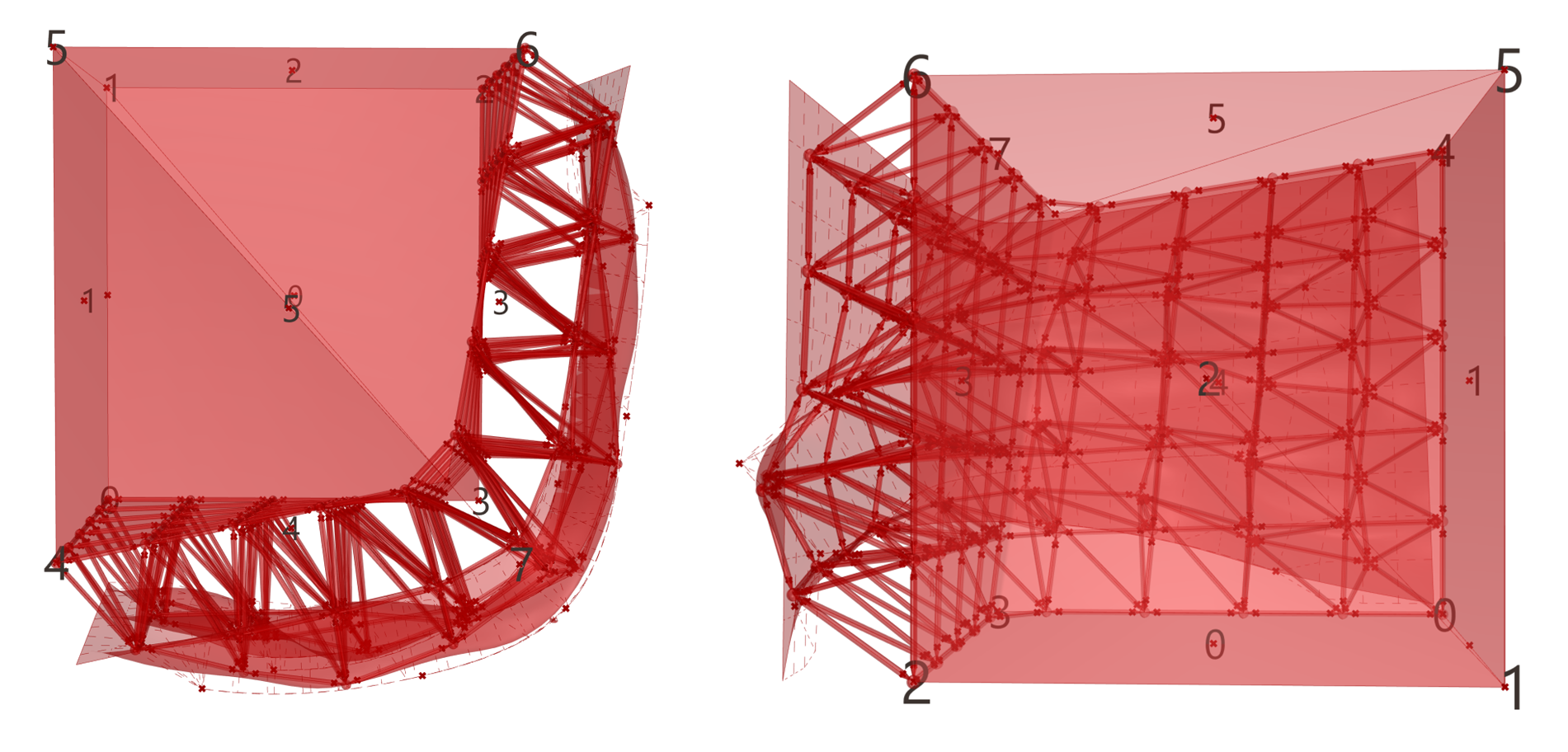
图 1.3.3-29 代码段(曲面)-14的结果
图 1.3.3-30 代码段(曲面)-14
⇩代码下载(codeSnippet_geometry_14.gh)
🍋🟩代码段-练习-15 ( )
较大尺度的区域性规划空间,不同功能区间的联系通常由道路确定。而景观中的道路形态有时也会更加自由,具有游戏性。本次练习构建一个简化版的道路辅助绘制工具道路面构建-简( 1.3.3-31)。通过道路轴线的点道路控制点输入参数,并指定道路宽度,及优化道路曲线形态的Smooth Strength和圆角Fillet Radius辅助快速的绘制道路。
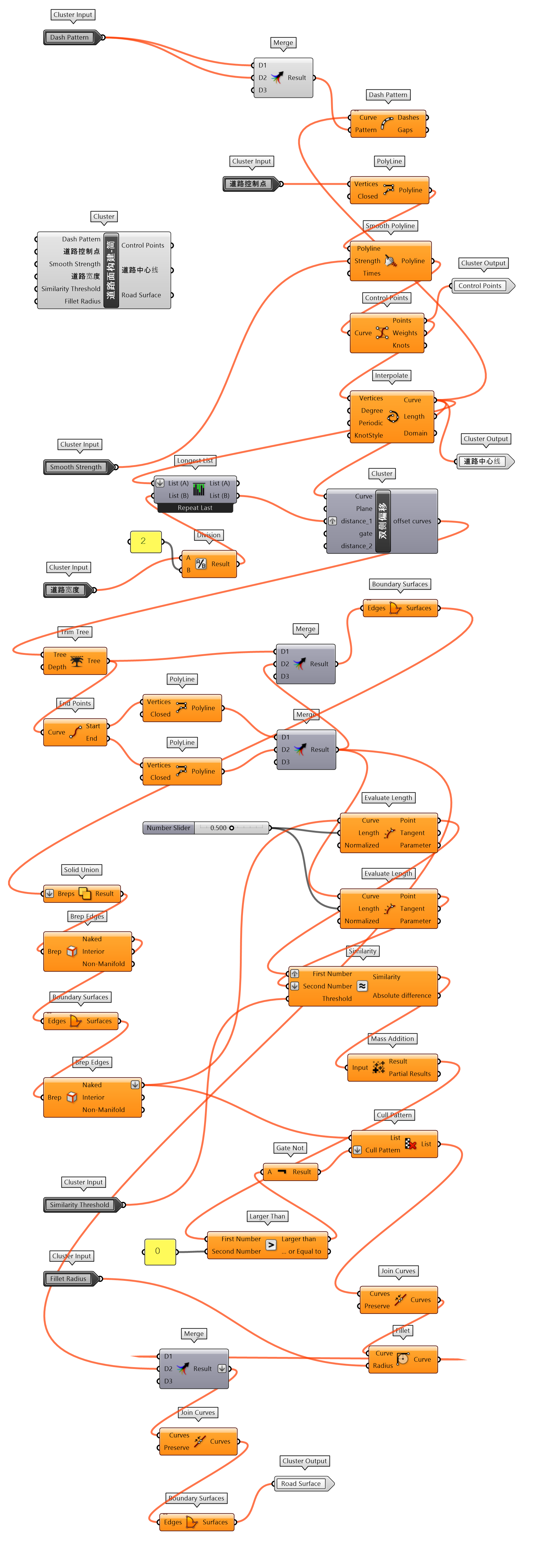
图 1.3.3-31 道路面构建-简 封装组件
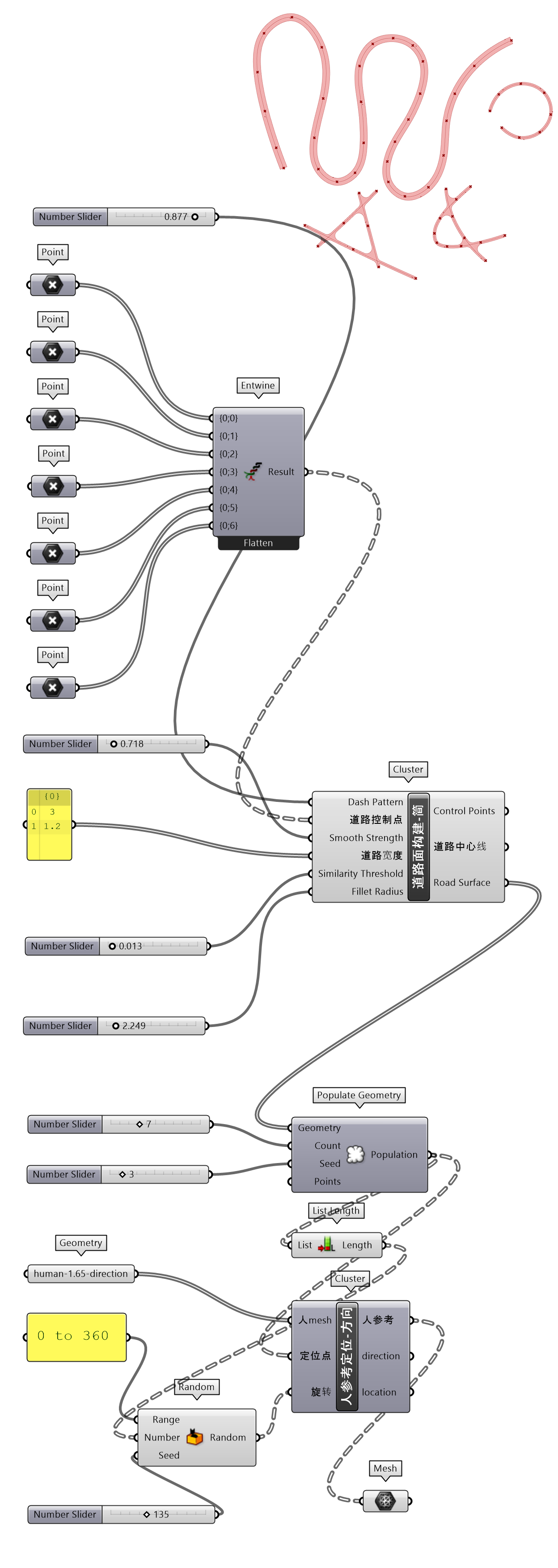
图 1.3.3-32 代码段(曲面)-15和结果
⇩代码下载(codeSnippet_geometry_15.gh)
🍋🟩代码段-练习-16 ( )
不同于练习10,应用盒体随机点磁场,将一个建筑表皮置于磁域;或练习11,将球体穿越磁域空间。图 1.3.3-33则是将整个设计场地置于这个磁域空间下,那么场地内的对象都可以应用这个磁域产生随机变化。这里构建了多个由“墙体,栅栏”半围合的空间,这些围护结构由封装的曲线的截面点组件(图 1.3.3-34_1)生成点,受磁域影响后通过点组织到体(图 1.3.3-34_2)构建的曲面而建立。曲线的截面点组件给出了两种构建截面的方法,圆或矩形。因为变化后的半围合对象的底面受磁域影响,并不是水平的,偏离了原始水平面,因此通过最低点的提取,依据最低点将对象移动到给定的原始水平面;同时场地的高程也进行了调整,将地形表面附着于半围合对象的变化底面。

图 1.3.3-33 代码段(曲面)-16的结果:动画
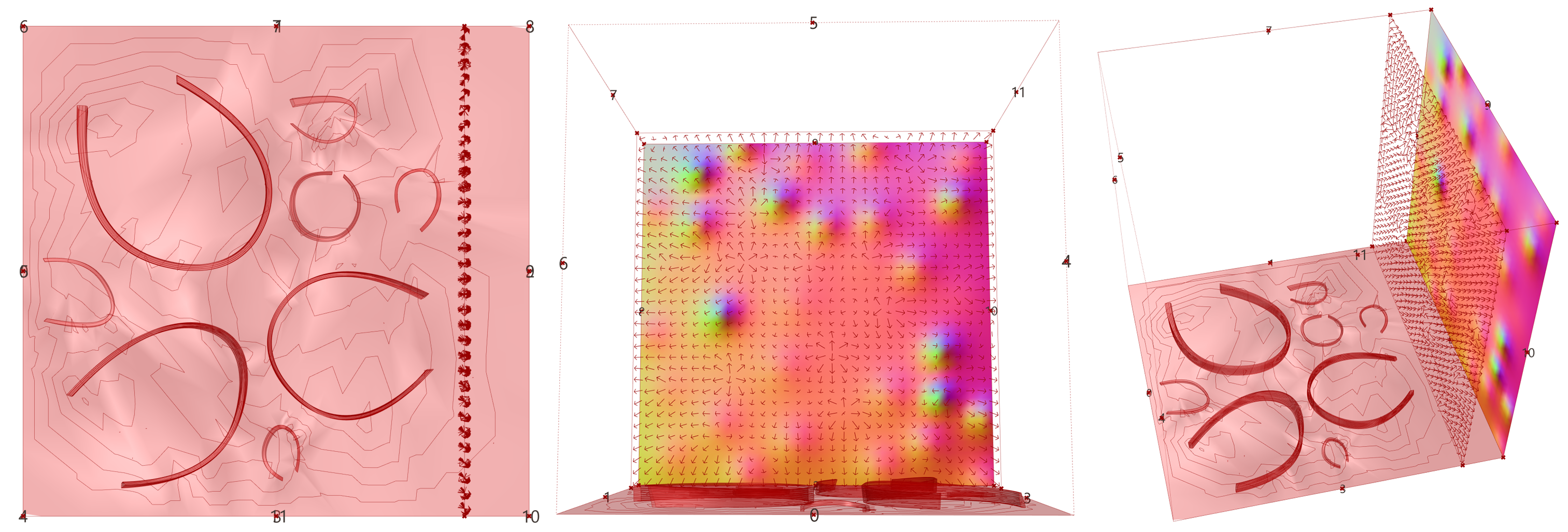
图 1.3.3-33 代码段(曲面)-16的结果
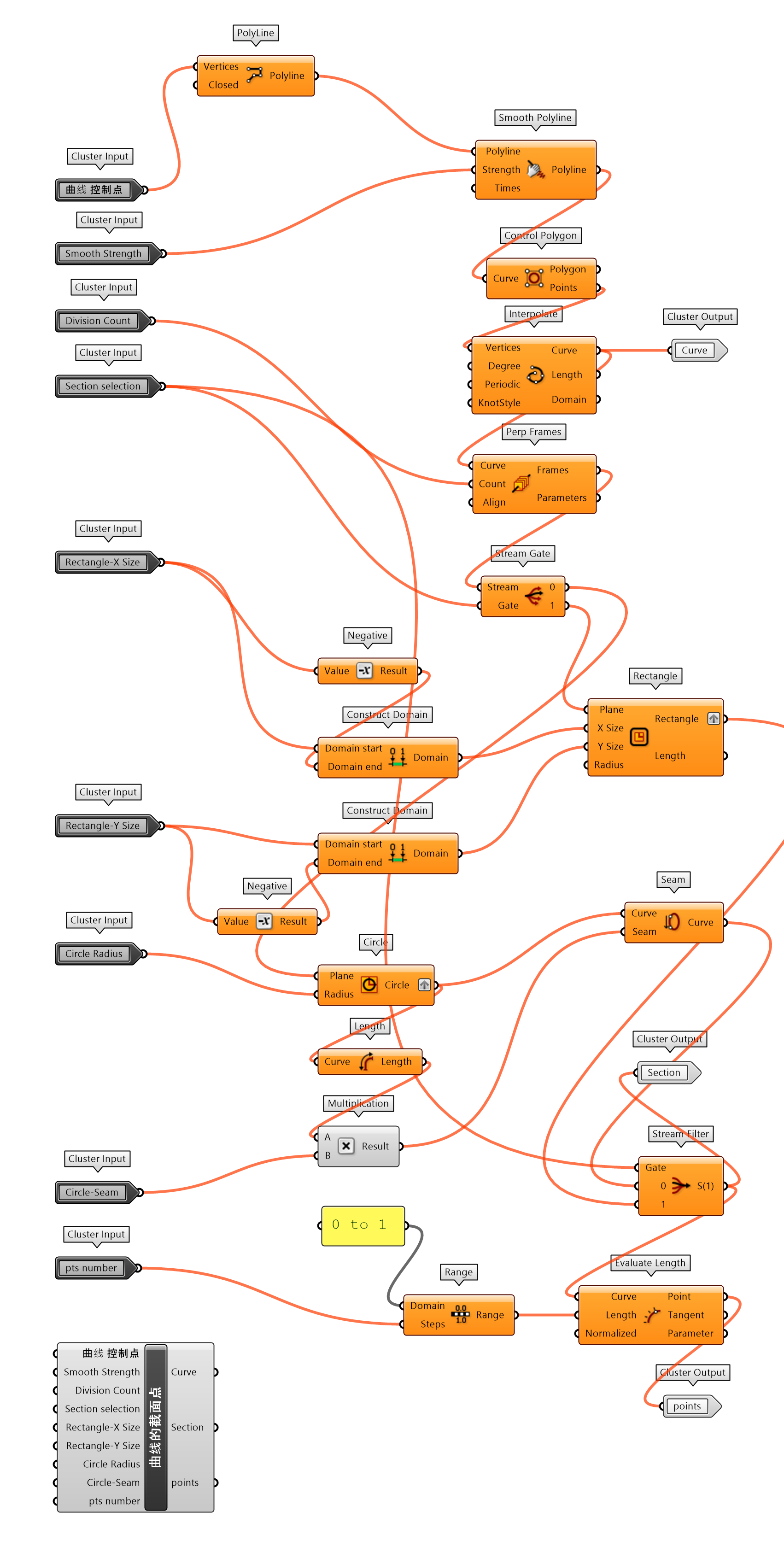
图 1.3.3-34_1 曲线的截面点 封装组件 |
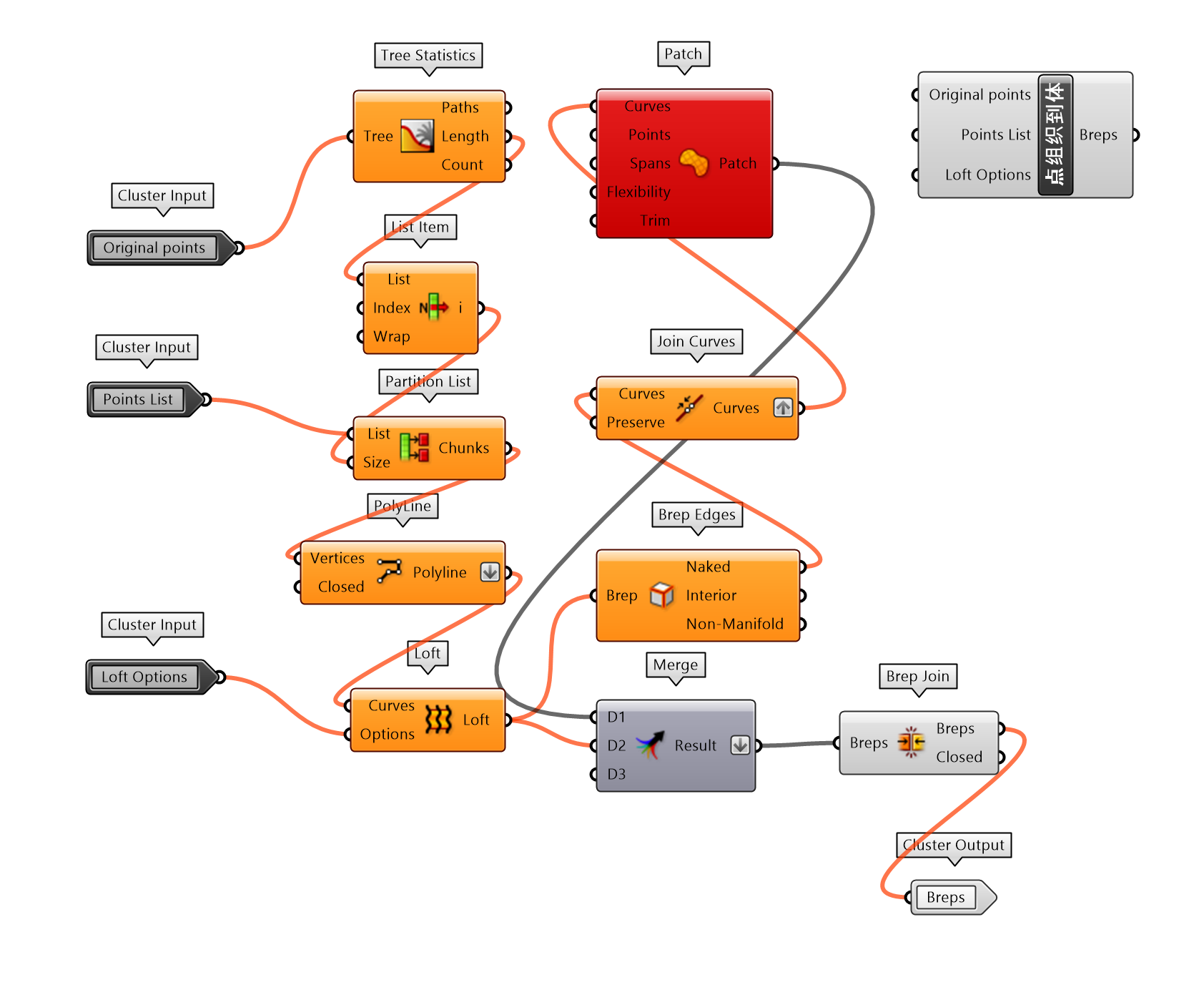
图 1.3.3-34_2 点组织到体 封装组件 |

图 1.3.3-35 代码段(曲面)-16
⇩代码下载(codeSnippet_geometry_16.gh)
🍋🟩代码段-练习-17 ( )
图 1.3.3-36 为曲面点线控制变化工具应用的又一个例子,不同于练习14变化的建筑表皮,这里要构筑一个具有雕塑感的座椅,或者雕塑艺术品。由曲线的截面点构建出管状对象控制点后,作为曲面点线控制变化的曲面点组输入参数,增加几条控制曲线和控制点,通过对其位置的调整和相关输入参数的变化,调试出图中的形态。调整后的对象仍然会发生位移,为将其置于给定标高,建立Z向相对移动工具(图 1.3.3-37),可以近似的将其重移回给定标高位置,代码如图 1.3.3-38。
因为曲面点线控制变化工具的辅助设计作用,整个形态的调整估计仅用10分钟,当然,如果需更准确的进行形态的塑造,则需更加细微的调整。

图 1.3.3-36 代码段(曲面)-17的结果
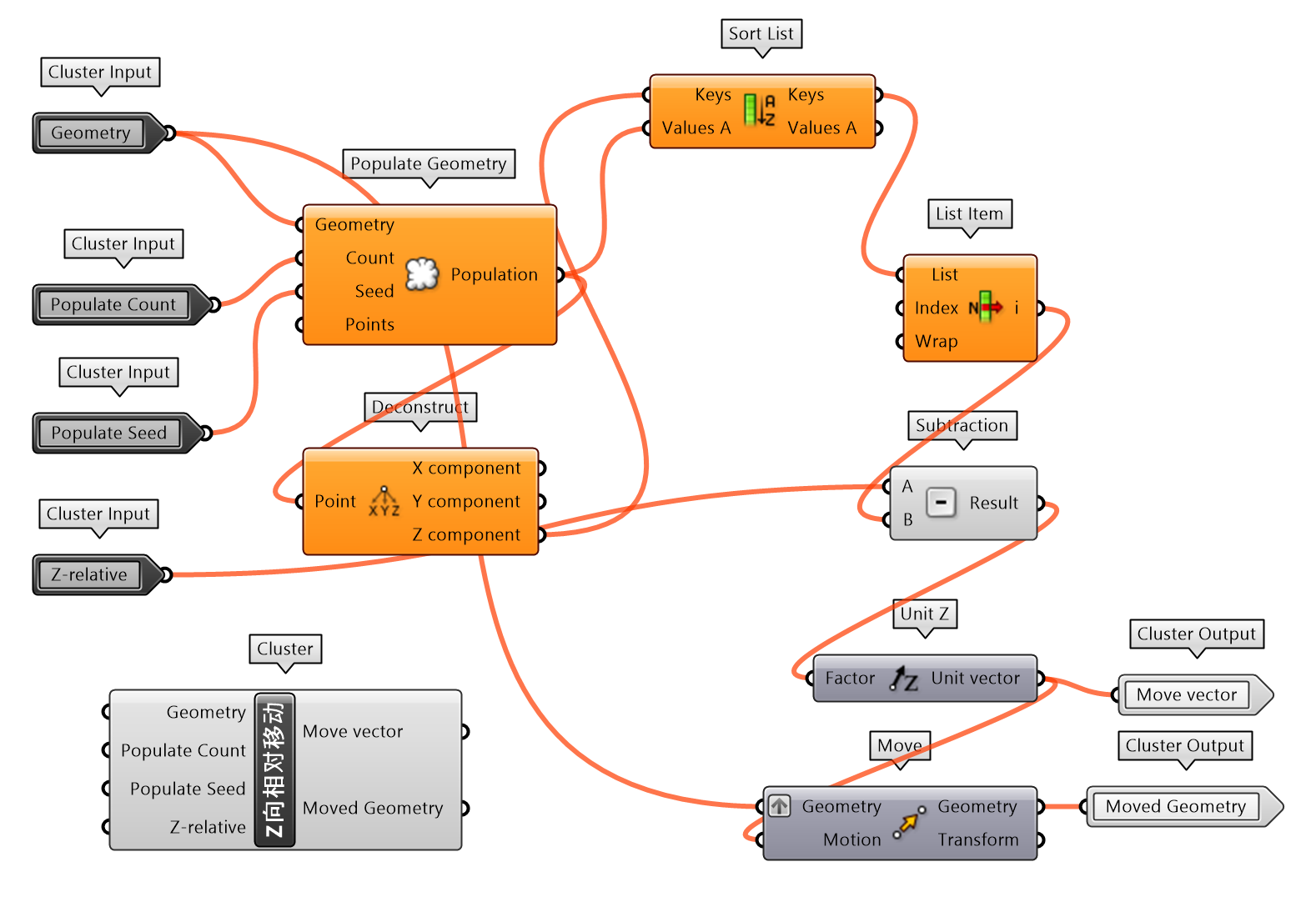
图 1.3.3-37 Z向相对移动 封装组件
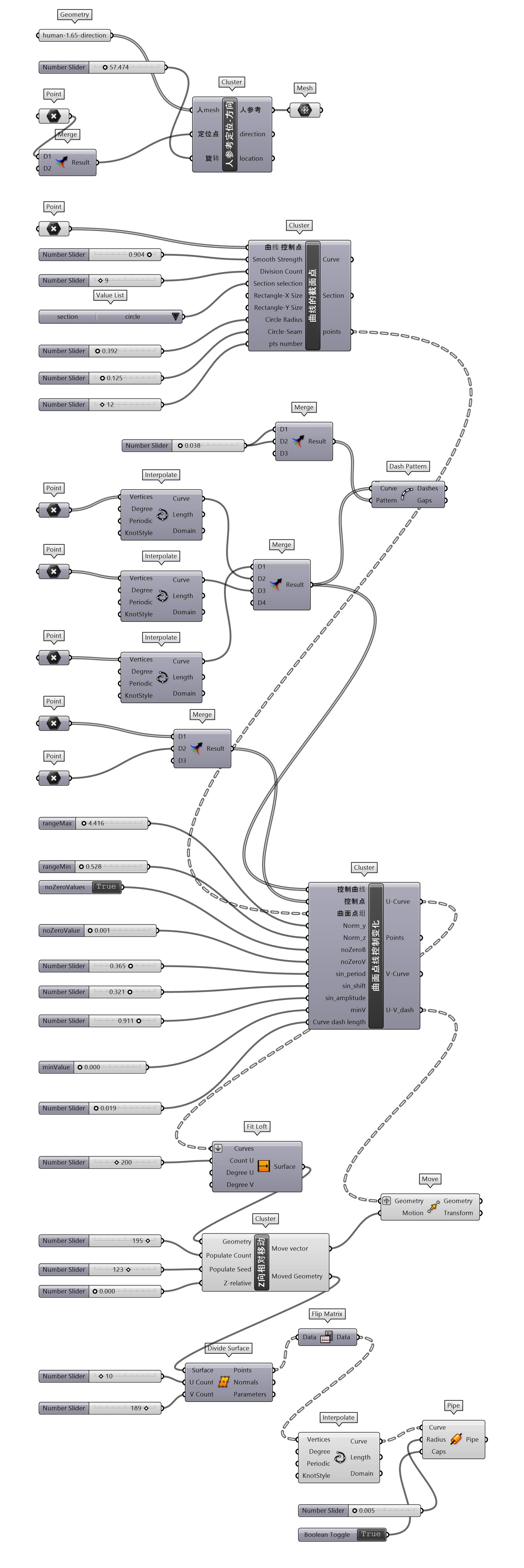
图 1.3.3-38 代码段(曲面)-17
⇩代码下载(codeSnippet_geometry_17.gh)
🍋🟩代码段-练习-18 ( )
调整曲面点线控制变化工具,在输出端移除了新曲面的相关属性,而调整为点受力大小的参数A,和标准化后的力大小参数A-remap,为曲面点线控制变化+力大小封装工具(图 1.3.3-39)。这样做的原因不是直接将吸引子产生的力直接作用于输入参数曲面点组对象,而是用于相关几何对象的调整上,例如图 1.3.3-40中变化十字的大小,进而裁切表皮,构建镂空十字形式,代码为图 1.3.3-41。
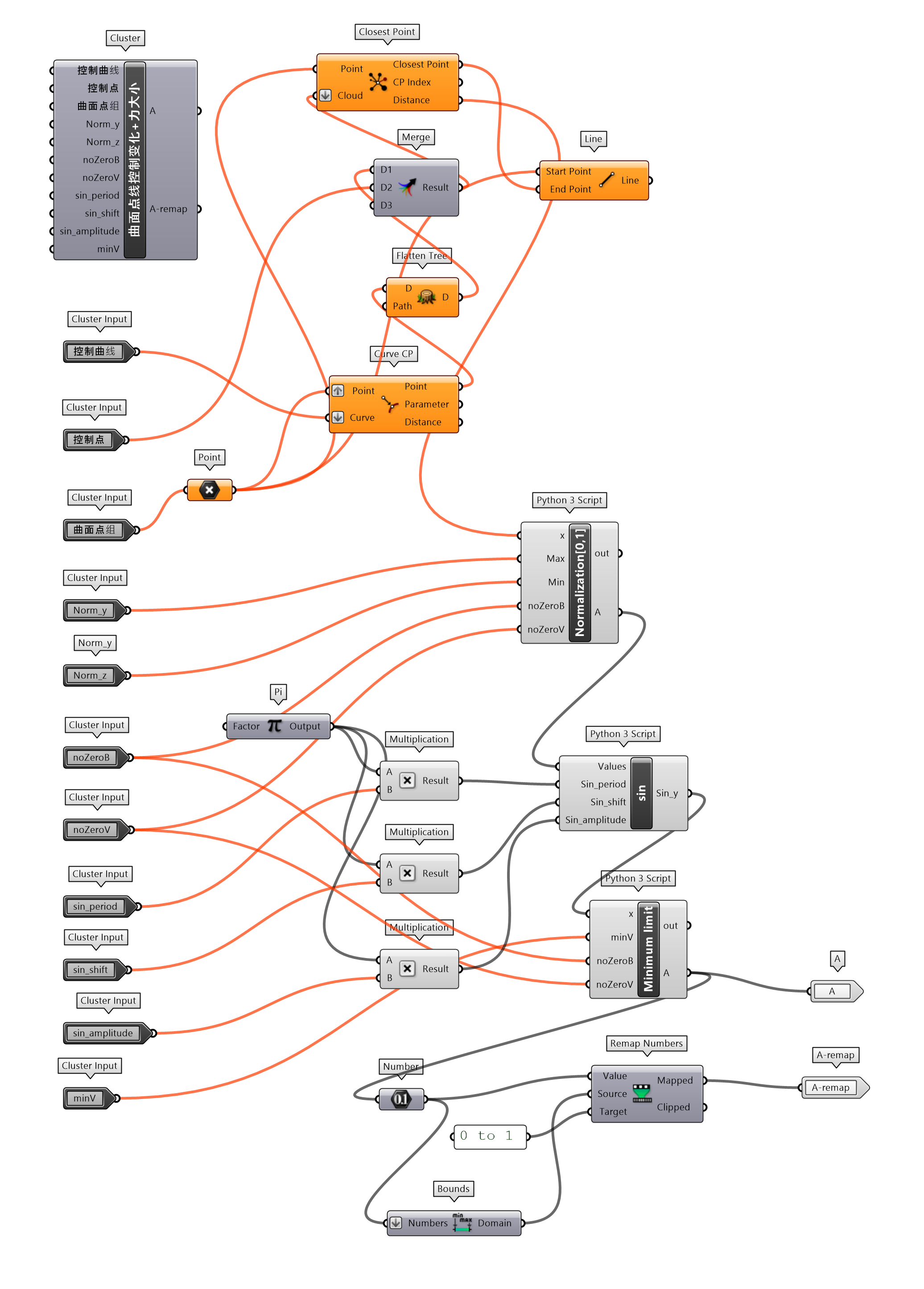
图 1.3.3-39 曲面点线控制变化+力大小 封装组件

图 1.3.3-40 代码段(曲面)-18的结果
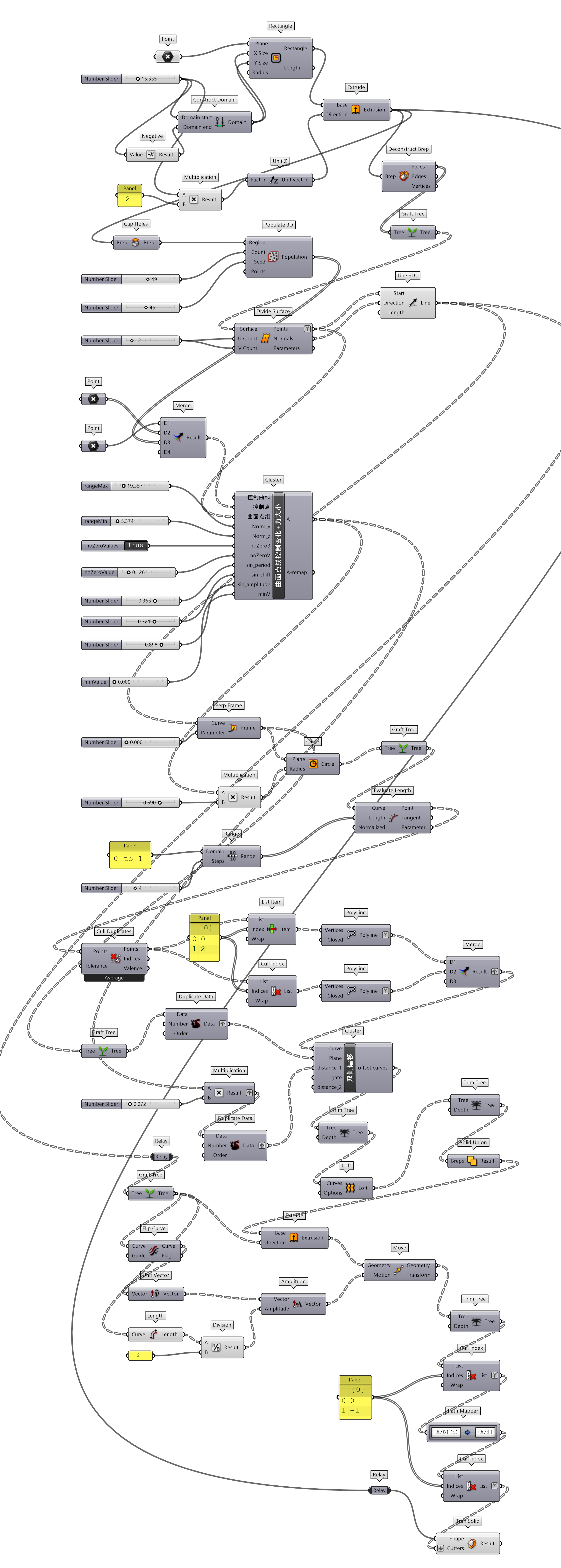
图 1.3.3-41 代码段(曲面)-18
⇩代码下载(codeSnippet_geometry_18.gh)
1.3.3.3 格网(Mesh)
Mesh 的单元特性(基本单元为三边面Triangle和四边面Quadrangle),使 Mesh 更适合用于幕墙等具有单元化特质的设计对象,方便单元形式的控制和细化,及加工建造。同时,Mesh 也是动力学组件kangaroo进行受力运动模拟的基本对象。因为单元特性,可以将单元格赋予光照、温湿度等序列值,因此也作为分析类(例如热环境分析Ladybug和Honeybee)连续表面数值可视化的基本载体;同地理信息化栅格数据格式,亦可用于地形的表达(单元格值或者顶点值为高程值),也可作为遥感影像的载体(单元格值或顶点值为波段值)。
在组织 Mesh (栅格)单元时,要确定三边面或四边面顶点的排序方式。如果构成 Mesh 的单元面很多,通常是利用曲线有序提取点,曲面有序提取点(例如 UV 点),再将这些有序点组织为单元面顶点,进而构建 Mesh 面。
🍋🟩代码段-练习-19 ( )
使用 1.3.1 代码段练习34中封装的Pts2MeshQuad组件,将盒体随机点磁场生成的点组织为Construct Mesh组件输入端Vertices的单元形式。而后编写MeshTopology和Flatten Box(Python Script),用于盒体 Mesh 对象的展平,其中MeshTopology是寻找盒体各个单元面的拓扑关系;Flatten Box则是依据单元面的拓扑关系使用递归的方法寻找盒体展平各单元面的展平顺序。盒体展平结果并不唯一,从图 1.3.3-42中可以看到对于同一盒体形态具有多种展平结果。通过 Mesh 面的索引值标识出各个单元面对应的位置,例如单元面9,其三边面边的尺寸分别为7.51、7.46和4.38,对位三维模型和展平的各个展平图,尺寸保持一致,也说明了展平结果的不唯一性。输入端LocationPoint为控制展平位置的三个点,最终代码如图 1.3.3-43。
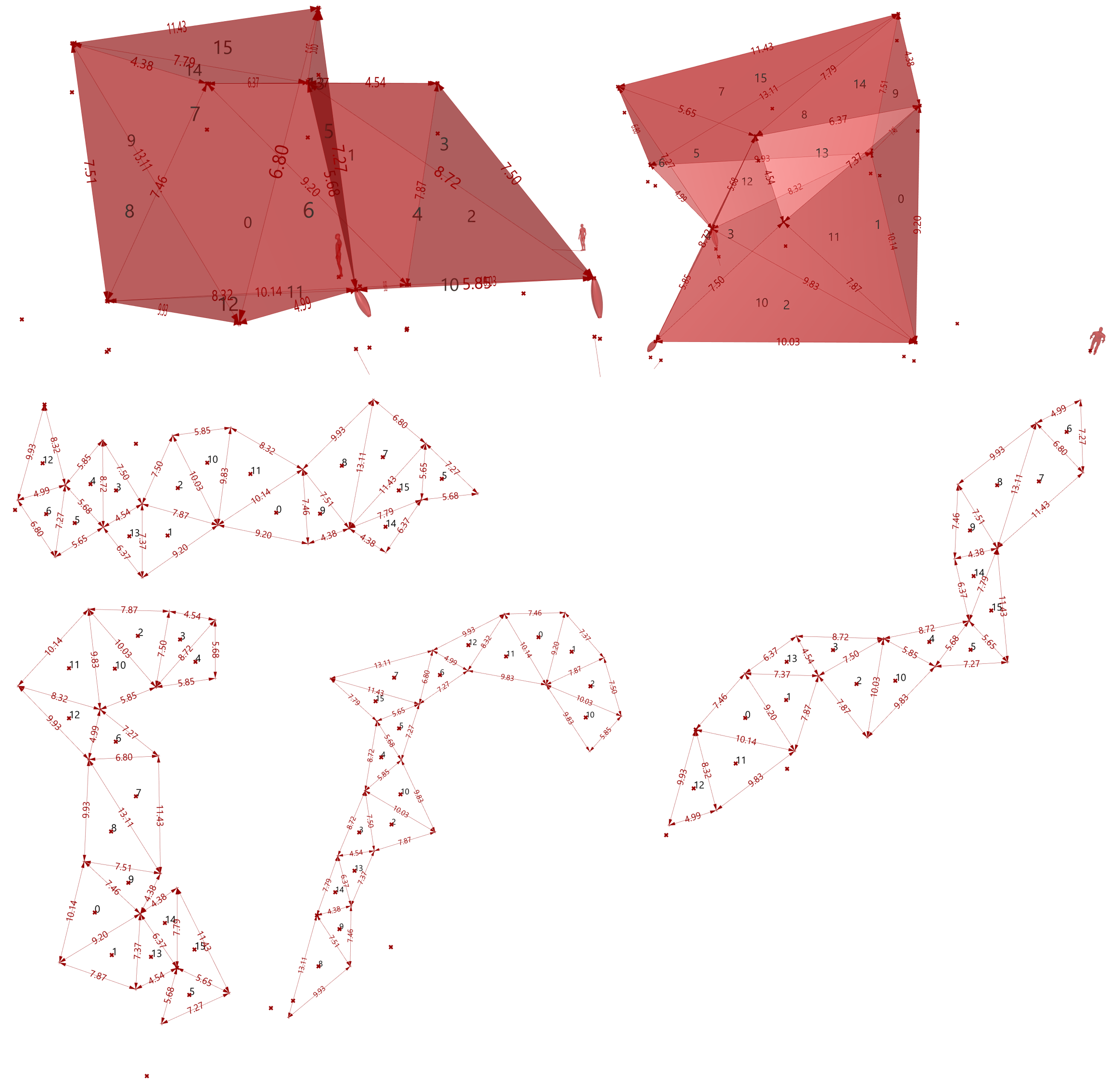
图 1.3.3-42 代码段(Mesh)-19的结果
图 1.3.3-43 代码段(Mesh)-19
MeshTopology(Python Script 组件)
'''
计算 Mesh 对象中每个单元面的拓扑关系(邻接单元面)
Inputs:
Mesh: Item[ghdoc Object]
输入的一个 Mesh 对象
Output:
MeshFlatten: Tree[Path,int]
每个单元面拓扑关系的返回列表
'''
import rhinoscriptsyntax as rs
import Rhino
import System
from Grasshopper import DataTree
from Grasshopper.Kernel.Data import GH_Path
def mesh_topology(mesh_join):
mesh = rs.ExplodeMeshes(mesh_join)
meshv = {}
for i in range(len(mesh)):
meshv[i] = rs.MeshVertices(mesh[i])
meshvkeys = list(meshv.keys())
meshvvalues = list(meshv.values())
tdic = {}.fromkeys(meshvkeys)
for i in meshvkeys:
tlist = []
a = meshvvalues[i]
for n in meshvvalues:
temp = []
for f in a:
if f in n:
temp.append(True)
tlist.append(temp)
tdic[i] = tlist
topologydic = {}.fromkeys(meshvkeys)
for i in meshvkeys:
b = tdic[i]
tempa = []
for j in range(len(b)):
if len(b[j]) == 2:
tempa.append(j)
topologydic[i] = tempa
MeshFlatten = DataTree[System.Int32]()
for i in meshvkeys:
path = GH_Path(i)
v = topologydic[i]
MeshFlatten.AddRange(v, path)
return MeshFlatten
if __name__ == "__main__":
MeshFlatten = mesh_topology(Mesh)
Flatten Box(Python Script 组件)
'''
将一个由 Mesh 面组成的盒体展品
Inputs:
Mesh: Item[Mesh]
带展平的盒体
MeshTopology: Tree[int,int]
盒体单元面的拓扑关系,可以用 MeshTopology 封装组件计算
LocationPoint: List[Point]
用于将单元面按拓扑关系展平在平面上的3个位置点
Finding: Bool
用于重新计算
Count: Int
用于配置每次寻找展平关系的循环次数
Output:
BoxFlatten: List[Mesh]
按展平顺序的 Mesh 单元面列表
OrderedMeshes: List[int]
按展平顺序的 Mesh 单元面索引值列表
'''
import rhinoscriptsyntax as rs
import Rhino
import System
import random
import copy
from Grasshopper import DataTree
from Grasshopper.Kernel.Data import GH_Path
import Grasshopper as gh
def topology_meshed():
'''
将 Tree 型数据类型的拓扑关系索引转换为字典格式
Returns
-------
Glst : Dict[int,List[int]]
单元面拓扑关系的字典格式.
'''
Glst = {}
for i in range(MeshTopology.BranchCount):
branchlst = MeshTopology.Branch(i)
lst = []
for k in range(len(branchlst)):
lst.append(branchlst[k])
Glst[i] = lst
return Glst
def order(allowlst, startmesh):
'''
使用递归的方法,寻找盒体展平的顺序
Parameters
----------
allowlst : Dict[int,List[int]]
为字典形式的单元面拓扑关系.
startmesh : Int
随机选择用于展平的第1个单元面.
Returns
-------
List[int]
盒体单元面展平的顺序.
'''
if len(allowlst) == 0:
return ordorlst
else:
ordorlst.append(startmesh)
tmesh = allowlst[startmesh]
allowlst.pop(startmesh)
if tmesh == []:
pass
else:
sidxt = random.choice(tmesh)
startmesh = sidxt
for i in list(allowlst.keys()):
if startmesh in allowlst[i]:
allowlst[i].remove(startmesh)
elif sidxt in allowlst[i]:
allowlst[i].remove(sidxt)
else:
pass
return order(allowlst, startmesh)
def flattenmesh(meshes, LocationPoint):
'''
按照盒体单元面展平的顺序,展平至二维平面
Parameters
----------
meshes : List[Mesh]
按照展平顺序提取的盒体单元面列表.
LocationPoint : List[Point]
将盒体展平到二维平面的定位点.
Returns
-------
xymeshes : List[Mesh]
展平后的盒体单元面.
'''
lp = []
for i in LocationPoint:
lp.append(rs.PointCoordinates(i))
xymeshes = []
for i in range(len(meshes)):
if i == 0:
mesh0point = rs.MeshVertices(meshes[i])
xymesh0 = rs.OrientObject(meshes[i], mesh0point, lp, 1)
xymeshes.append(xymesh0)
else:
vertices2 = rs.MeshVertices(meshes[i])
vertices1 = rs.MeshVertices(meshes[i-1])
ver = [m for m in vertices1 for n in vertices2 if m == n]
a = ver[0]
b = ver[1]
indexa = vertices1.index(a)
indexb = vertices1.index(b)
d = [m for m in vertices2 if m not in ver][0]
refvertice = rs.MeshVertices(xymeshes[i-1])
indexc = [c for c in range(0, 3) if c != indexa and c != indexb]
refverticespoint = rs.MirrorObject(rs.AddPoint(
refvertice[indexc[0]]), refvertice[indexa], refvertice[indexb])
mirrorpoint = rs.PointCoordinates(refverticespoint)
xymesh = rs.OrientObject(meshes[i], [a, b, d], [
refvertice[indexa], refvertice[indexb], mirrorpoint], 1)
xymeshes.append(xymesh)
vertices2lst = []
vertices1lst = []
ver = []
return xymeshes
if __name__ == "__main__":
mesh = rs.ExplodeMeshes(Mesh)
Glst = topology_meshed()
OrderedMeshes = None
for k in range(int(Count)):
try:
ordorlst = []
allowlst = copy.deepcopy(Glst)
startmesh = random.choice(list(allowlst.keys()))
OrderedMeshes = order(allowlst, startmesh)
except KeyError:
pass
finally:
if OrderedMeshes is not None:
break
if OrderedMeshes is not None:
ordermesh = [mesh[i] for i in OrderedMeshes]
BoxFlatten = flattenmesh(ordermesh, LocationPoint)
print("Get a solution...")
else:
print("Order is None...")
⇩代码下载(codeSnippet_geometry_19.gh)
🍋🟩代码段-练习-20 ( )
练习19是盒体展平,图 1.3.3-44练习则是非闭合的 Mesh “曲面”展平。展平的方法同Flatten Box中定义的flattenmesh函数,将其提取出来单独定义为展平Mesh(Python Script 组件)。需要注意,不管是盒体展平,还是非闭合 Mesh 展平,都需要输入端的 Mesh 类型为三边面,确保单元为平面。如果原有四边面也为平面,并且加工时需要保持四边面的形态,则可以先转为三边面后,再由展平结果根据索引值重新组织回四边面。代码为图 1.3.3-45。

图 1.3.3-44 代码段(Mesh)-20的结果

图 1.3.3-45 代码段(Mesh)-20
展平Mesh (Python Script 组件)
'''
将条形的 Mesh 单元面展平到二维平面
Inputs:
Mesh: Tree[Mesh]
多个条形的 Mesh 单元
LocationPoint:List[Point]
用于将单元面按拓扑关系展平在平面上的3个位置点
Output:
FlattenMeshes: List[Mesh]
展平的 Mesh 对象
'''
import rhinoscriptsyntax as rs
import Rhino
from Grasshopper import DataTree
from Grasshopper.Kernel.Data import GH_Path
def flattenmesh(mesh, LocationPoint):
lp = []
for i in LocationPoint:
lp.append(rs.PointCoordinates(i))
meshes = rs.ExplodeMeshes(mesh)
xymeshes = []
for i in range(len(meshes)):
if i == 0:
mesh0point = rs.MeshVertices(meshes[i])
xymesh0 = rs.OrientObject(meshes[i], mesh0point, lp, 1)
xymeshes.append(xymesh0)
else:
vertices2 = rs.MeshVertices(meshes[i])
vertices1 = rs.MeshVertices(meshes[i-1])
ver = [m for m in vertices1 for n in vertices2 if m == n]
a = ver[0]
b = ver[1]
indexa = vertices1.index(a)
indexb = vertices1.index(b)
d = [m for m in vertices2 if m not in ver][0]
refvertice = rs.MeshVertices(xymeshes[i-1])
indexc = [c for c in range(0, 3) if c != indexa and c != indexb]
refverticespoint = rs.MirrorObject(rs.AddPoint(
refvertice[indexc[0]]), refvertice[indexa], refvertice[indexb])
mirrorpoint = rs.PointCoordinates(refverticespoint)
xymesh = rs.OrientObject(meshes[i], [a, b, d], [
refvertice[indexa], refvertice[indexb], mirrorpoint], 1)
xymeshes.append(xymesh)
vertices2lst = []
vertices1lst = []
ver = []
return xymeshes
if __name__ == "__main__":
Glst = []
fglst = []
for i in range(Mesh.BranchCount):
branchlst = Mesh.Branch(i)
lst = []
for k in range(len(branchlst)):
lst.append(branchlst[k])
joinmesh = rs.JoinMeshes(lst, True)
Glst.append(joinmesh)
FlattenMeshes = []
for i in Glst:
flst = flattenmesh(i, LocationPoint)
FlattenMeshes.append(rs.JoinMeshes(flst, True))
⇩代码下载(codeSnippet_geometry_20.gh)
🍋🟩代码段-练习-21 ( )
图 1.3.3-46为使用梭柱封装组件调整形态,提取曲面 UV 点后,移动组织该 UV 点,并由Pts2MeshQuad配合Construct Mesh构建 Mesh 的过程。

图 1.3.3-46 代码段(Mesh)-21和结果
⇩代码下载(codeSnippet_geometry_21.gh)
🍋🟩代码段-练习-22 ( )
将传统的建筑形式加入现代的设计元素,似乎能够让淳朴的设计传递出时尚的气息。图 1.3.3-47将传统米仓的墙体开窗为 Mesh 空间变化的三边面幕墙,并将内部的吧台转换为异形形态。建筑参数化模型的建构,也将主要的构建对象封装为单独的组件,方便类似设计的使用,首先进一步简化人参考定位为人参考定位-随机旋转(图 1.3.3-48_1),避免每次调用时需要编写旋转输入参数;还包括米仓-压顶(图 1.3.3-48_2)、洞口-改-周期(图 1.3.3-48_3)、米仓屋顶(图 1.3.3-48_4)、吧台-A(图 1.3.3-48_5)、幕墙-随机变化三边面(图 1.3.3-48_6)等。最终代码为图 1.3.3-49。
`幕墙-随机变化三边面`封装组件,因为表面点垂直和切向参考平面的变化不确定性,其普适性较弱,可以进一步调整参数化建构逻辑,使其适用于不同的曲面生成同样逻辑的设计形态。

图 1.3.3-47 代码段(Mesh)-22的结果
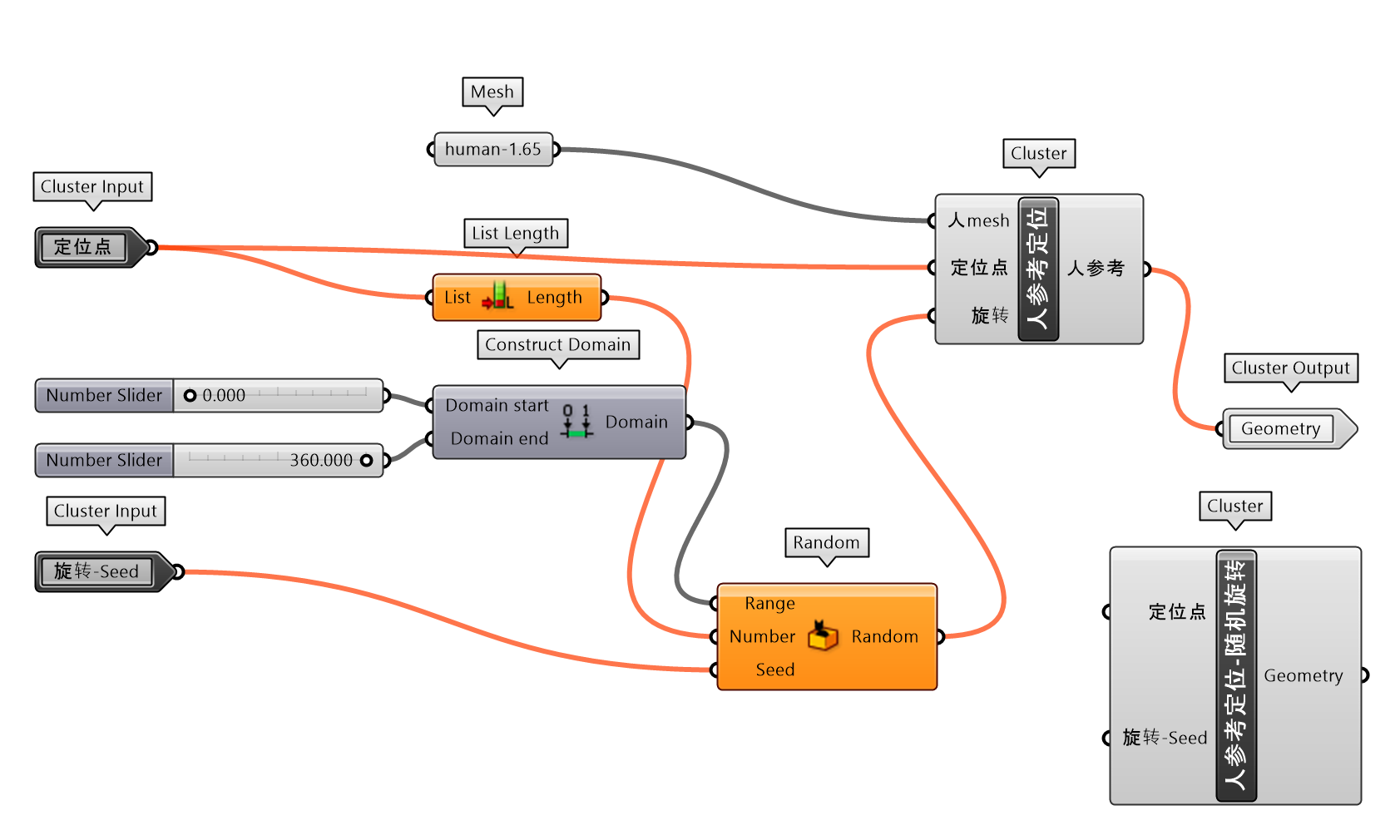
图 1.3.3-48_1 人参考定位-随机旋转 封装组件 |
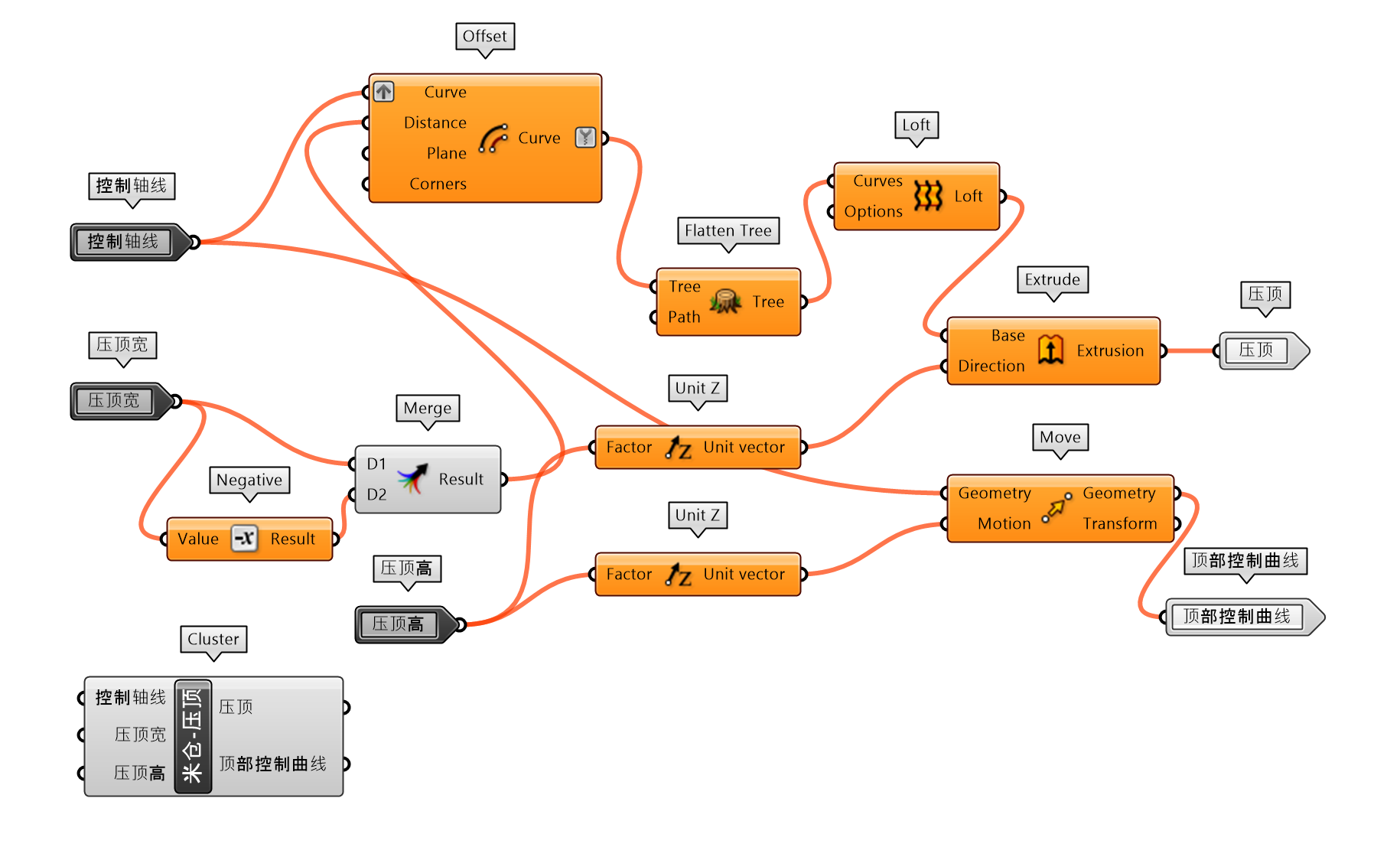
图 1.3.3-48_2 米仓-压顶 封装组件 |
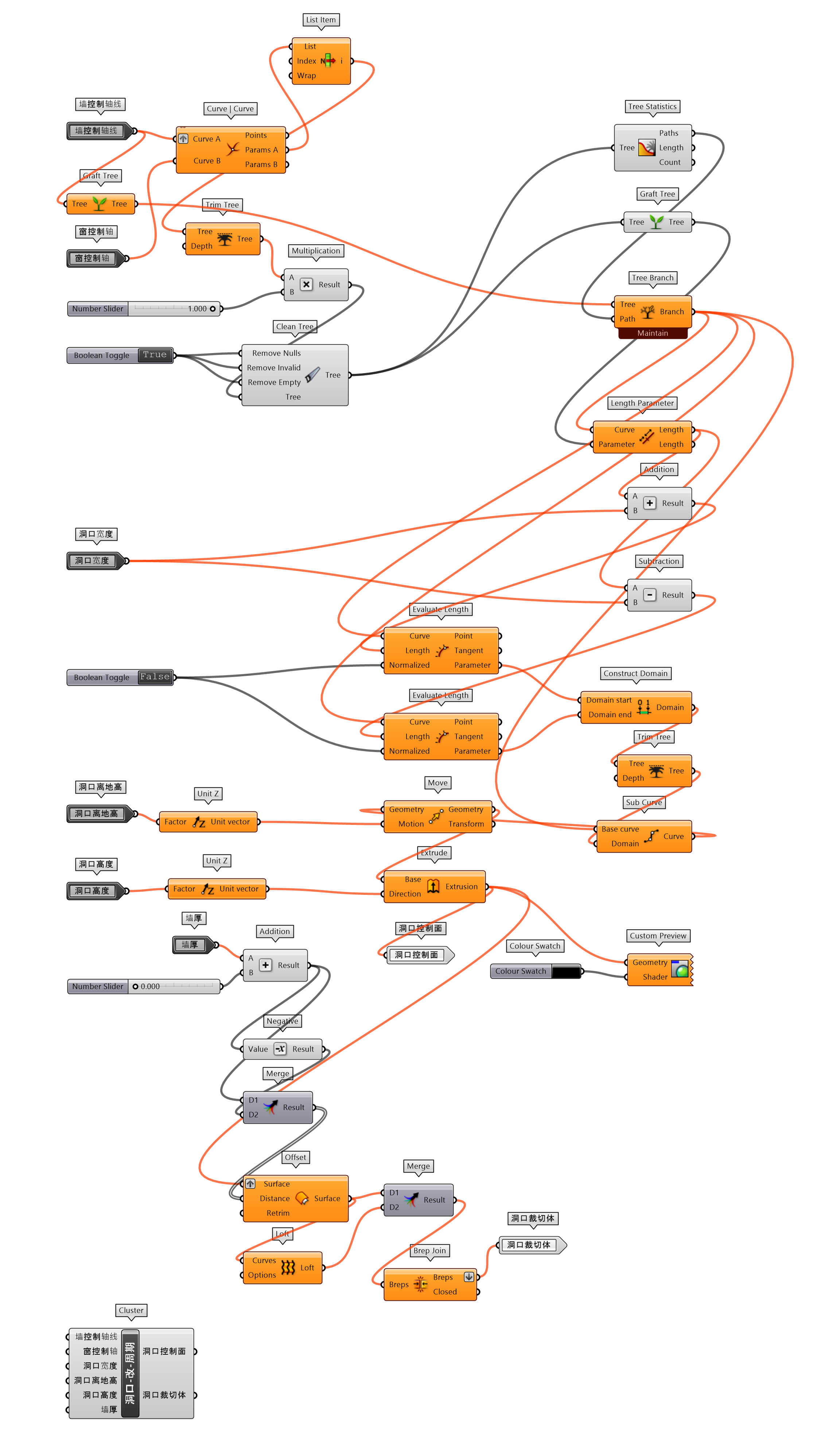
图 1.3.3-48_3 洞口-改-周期 封装组件 |
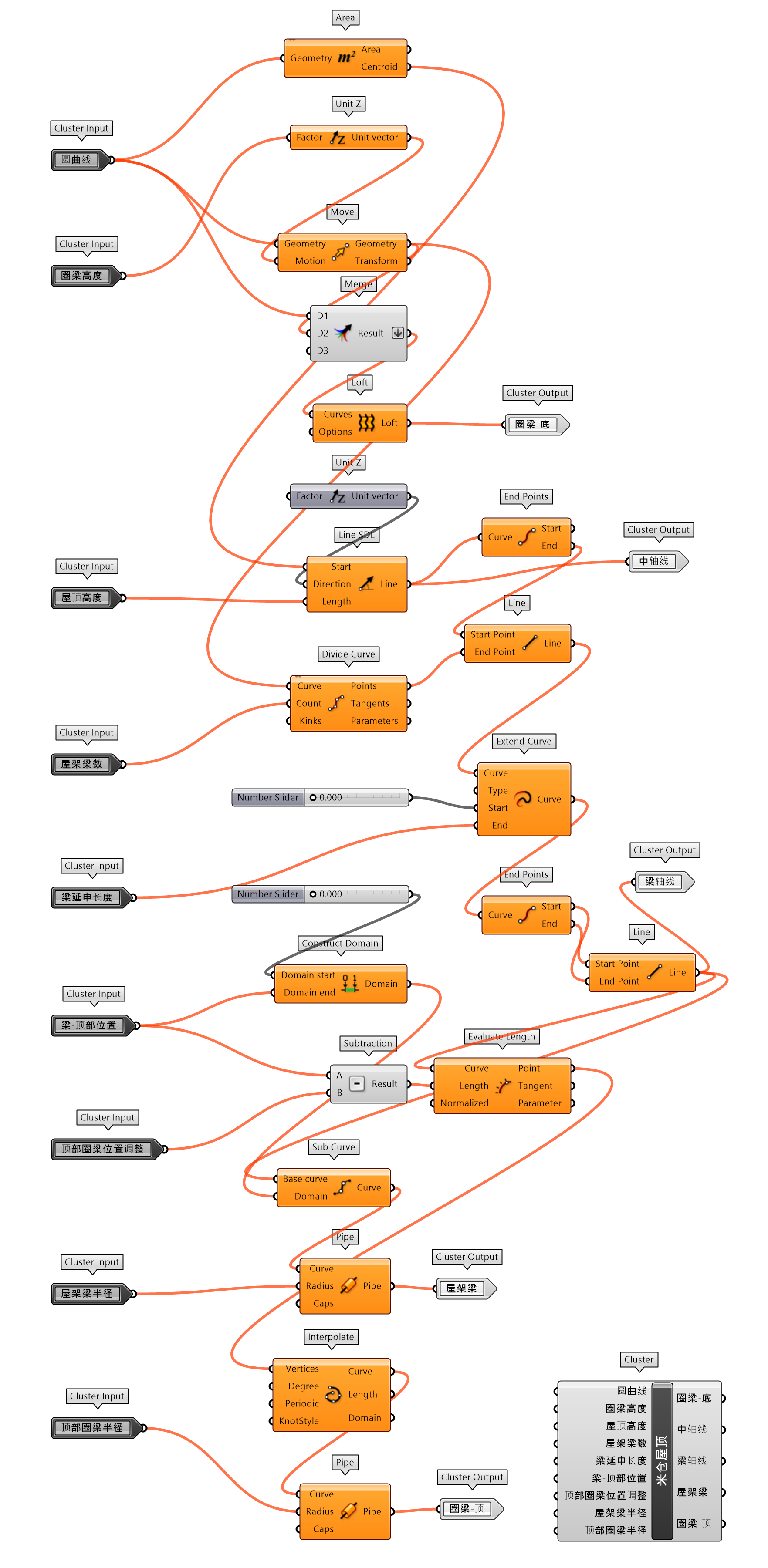
图 1.3.3-48_4 米仓屋顶 封装组件 |
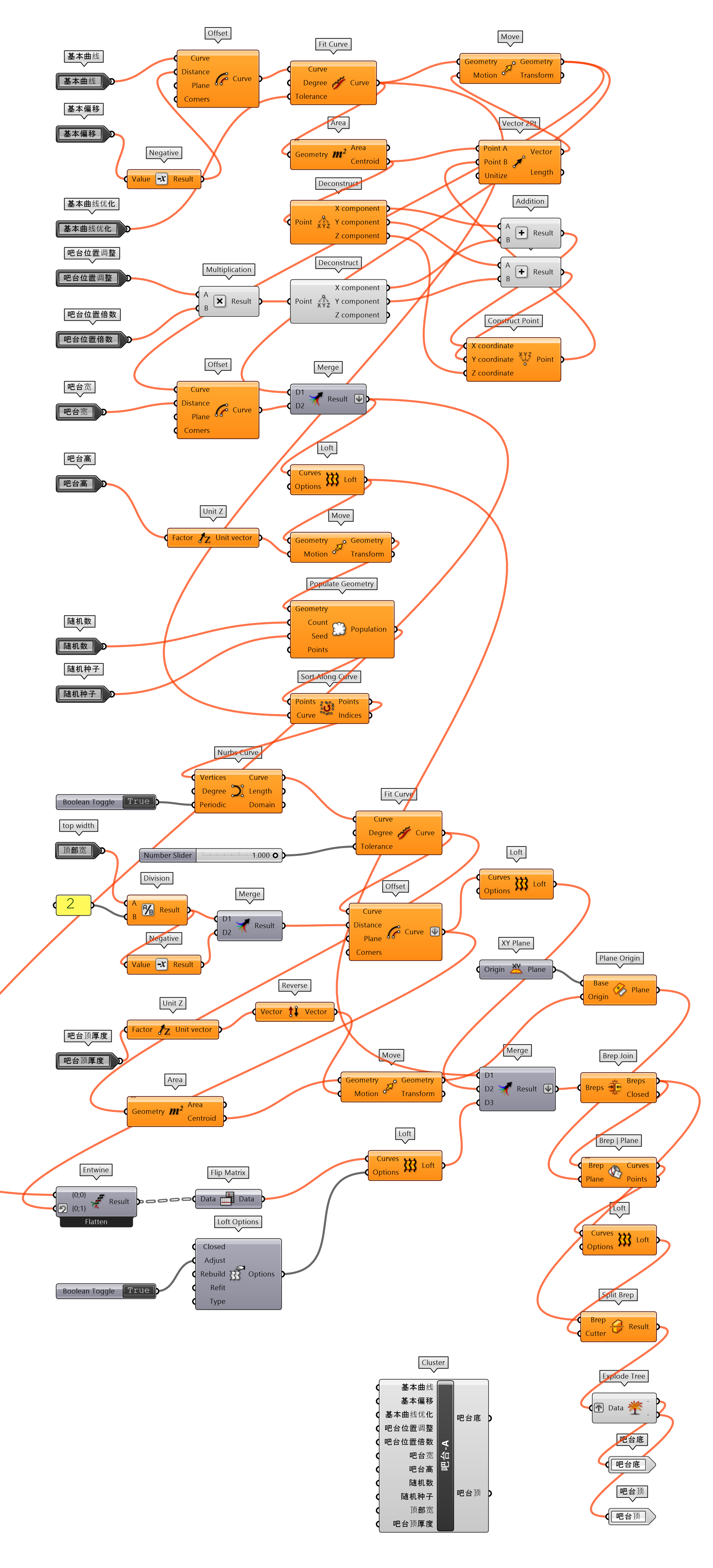
图 1.3.3-48_5 吧台-A 封装组件 |
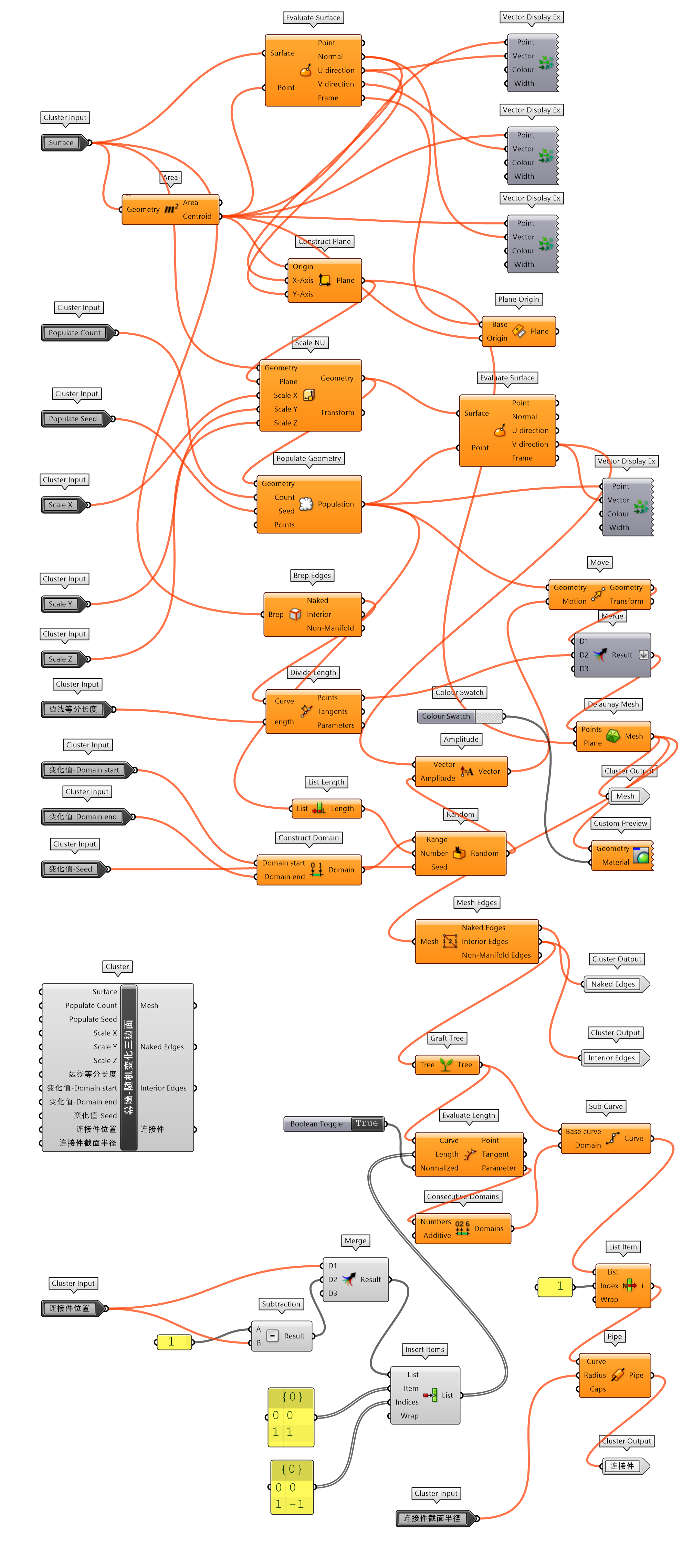
图 1.3.3-48_6 幕墙-随机变化三边面 封装组件 |

图 1.3.3-49 代码段(Mesh)-22
⇩代码下载(codeSnippet_geometry_22.gh)
🍋🟩代码段-练习-23 ( )
图 1.3.3-50是细节设计的一个练习,为深化幕墙(表皮)单元连接件的设计,其参数化设计的逻辑继承了练习14中对于桁架的处理方式。幕墙支撑-A(图 1.3.3-51)给出了两个输入条件,即是否Normalized标准化,为Evaluate Length的Normalized输入端参数。当为实际输入尺寸时,各个连接件的长度是相同的(图 1.3.3-50左);当为[0,1]输入参数时,是按边的比例提取连接件的长度,因此可以看到连接件长度的变化(图 1.3.3-50右)。最终代码如图 1.3.3-52。
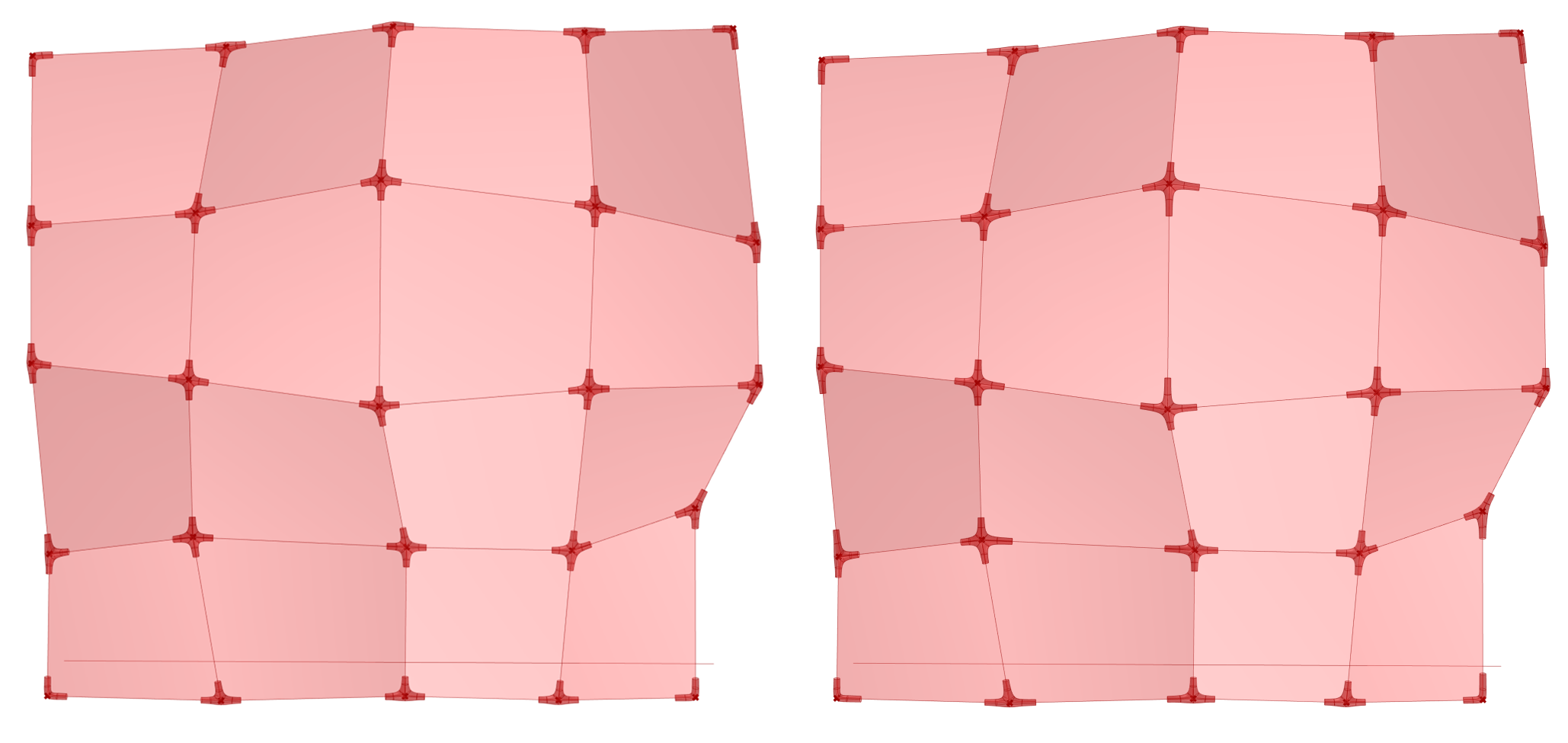
图 1.3.3-50 代码段(Mesh)-23的结果
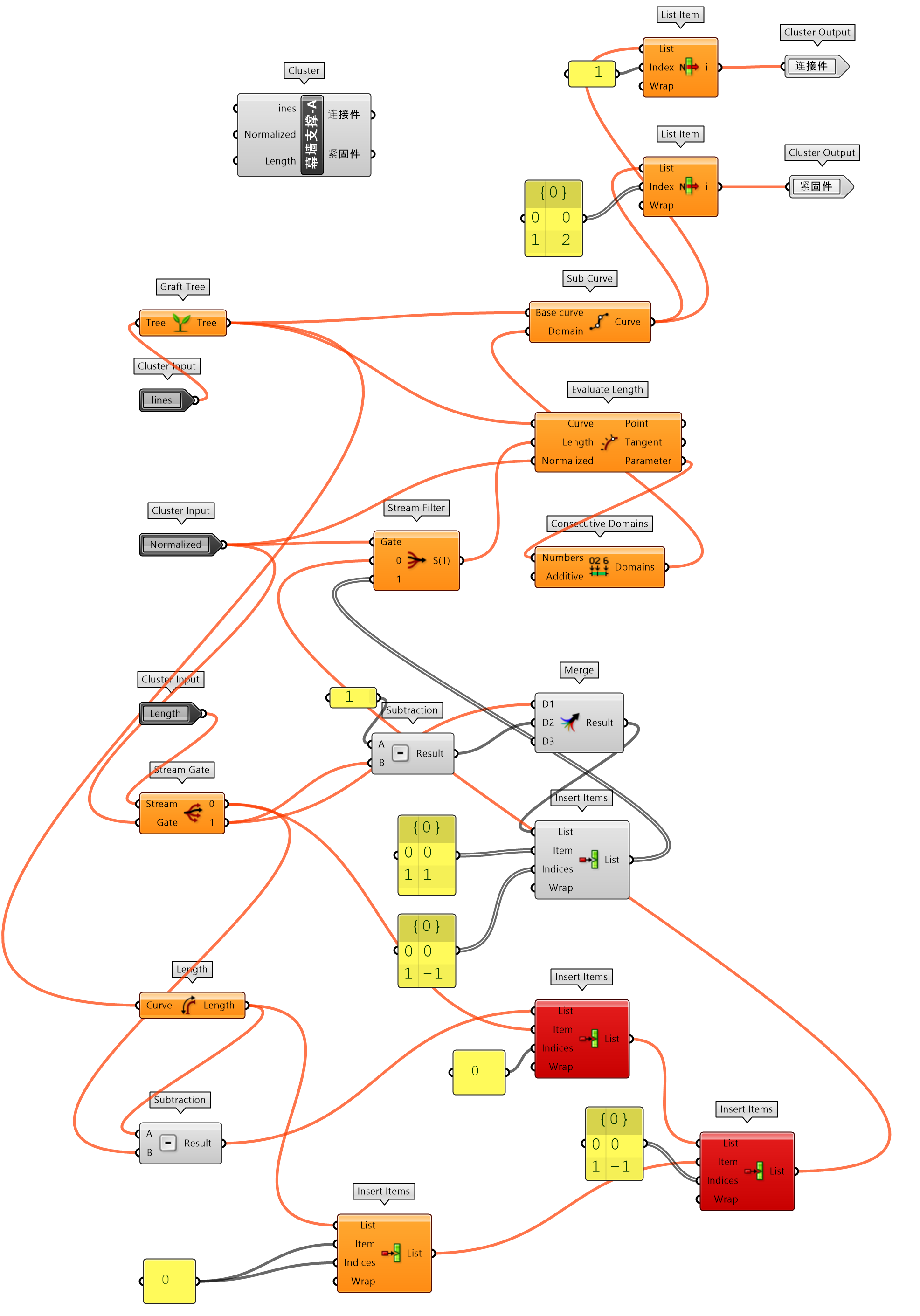
图 1.3.3-51 幕墙支撑-A 封装组件
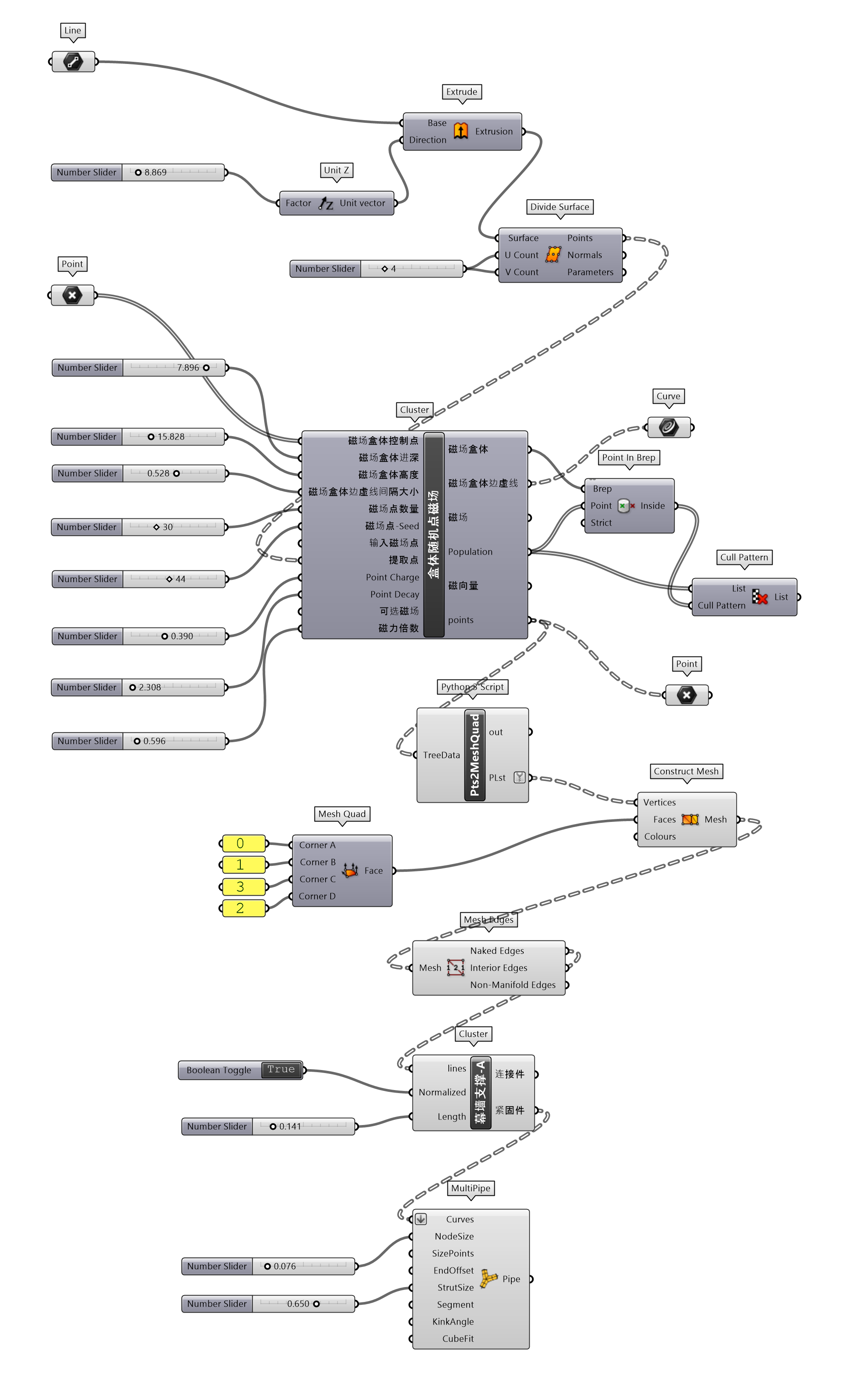
图 1.3.3-52 代码段(Mesh)-23
⇩代码下载(codeSnippet_geometry_23.gh)
🍋🟩代码段-练习-24 ( )
构建的曲面点线控制变化工具可以应用到场地(广场)的设计当中,如图 1.3.3-53,通过对地表的雕刻,设计出具有大地艺术性质的空间。工具的使用,避免逐根调整设计结构线,并在单元间构建了连续变化的关系,使得设计的效率得以大幅度提升。这些结构线也可以进一步编程为自动生成的方式,那么场地的雕刻会产生无数种形式结果,这里不再赘述,代码如图 1.3.3-54。
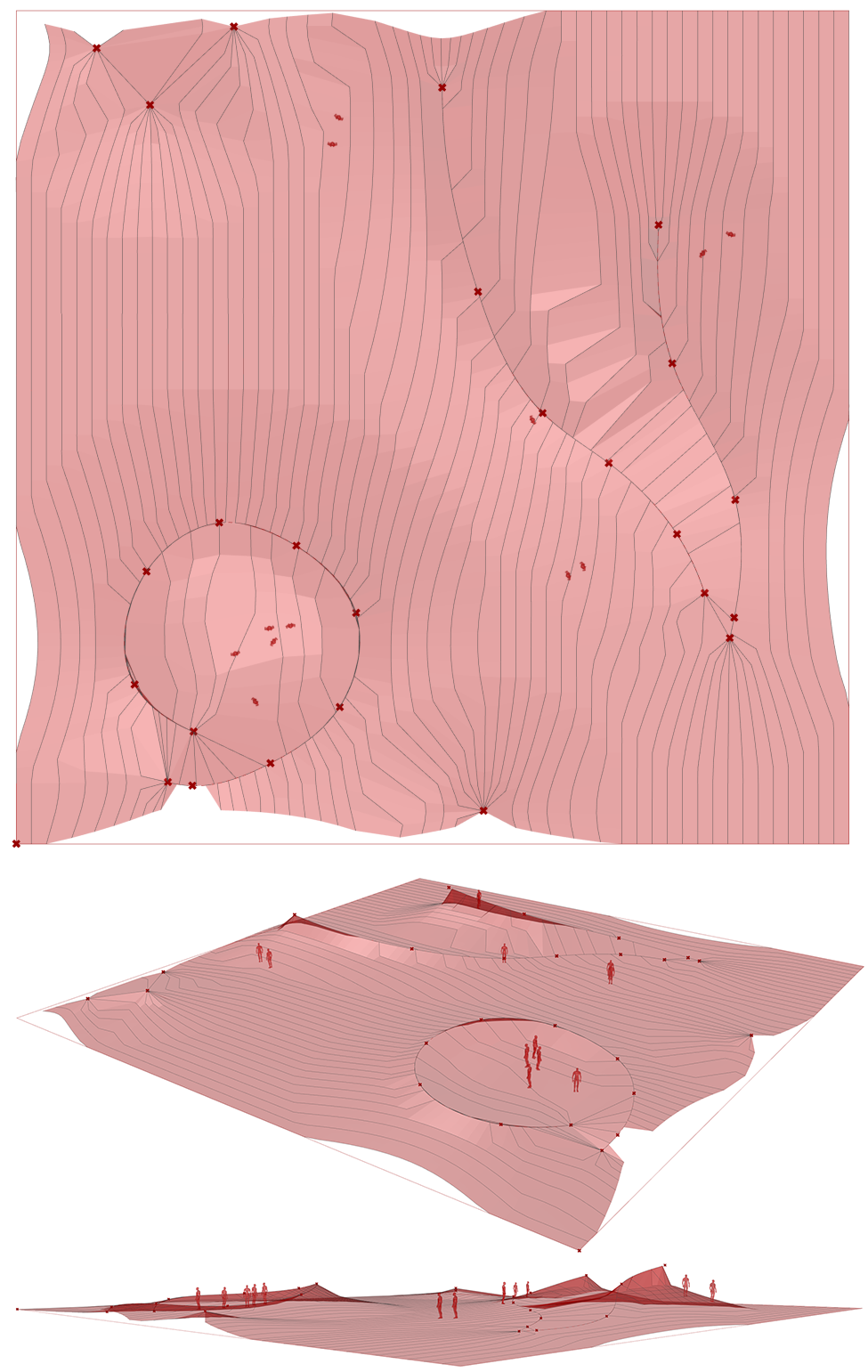
图 1.3.3-53 代码段(Mesh)-24的结果
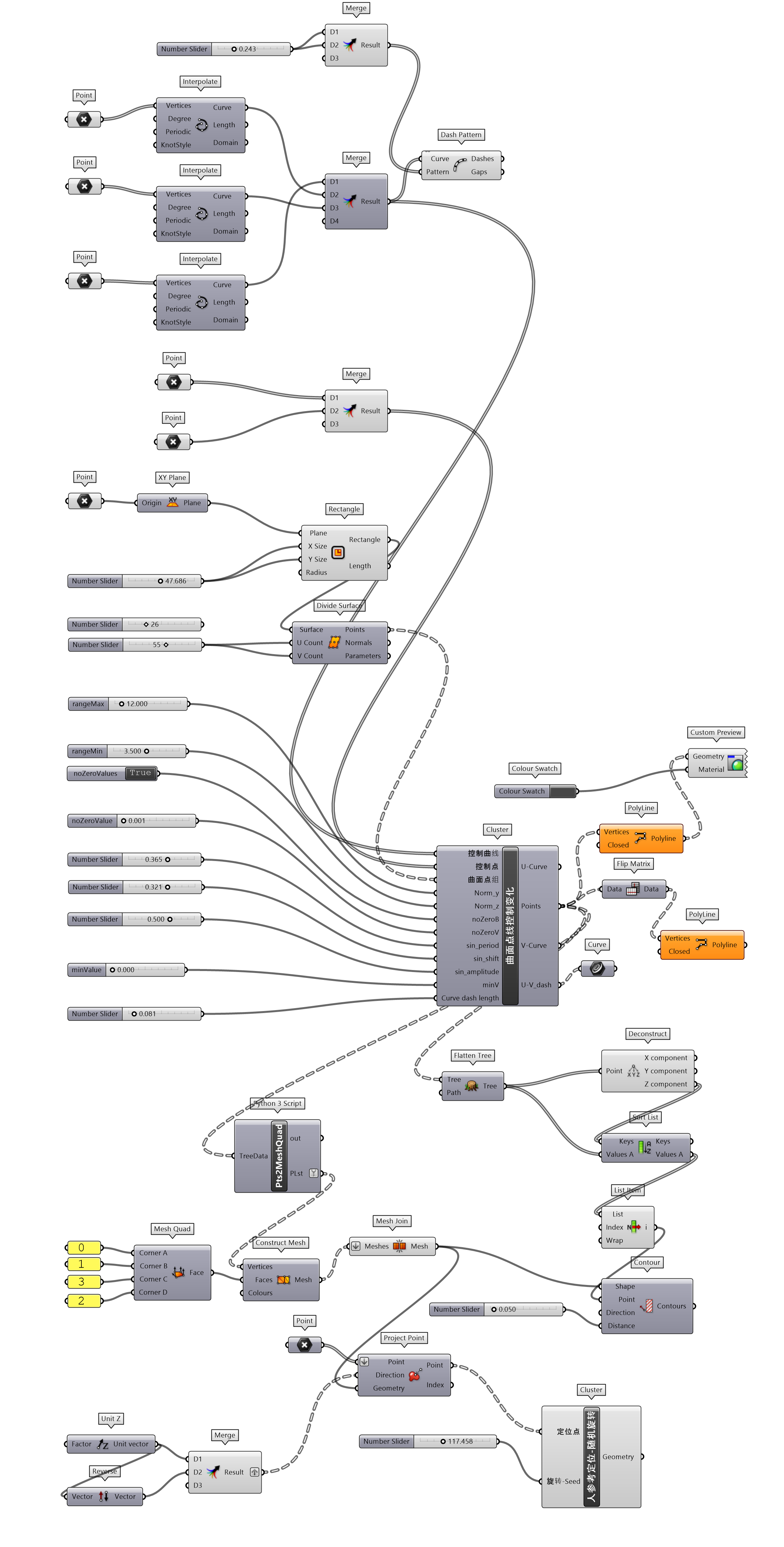
图 1.3.3-54 代码段(Mesh)-24
⇩代码下载(codeSnippet_geometry_24.gh)
🍋🟩代码段-练习-25 ( )
除了非闭合形式的表皮(Mesh 类)处理,半闭合或全闭合表皮塑造的空间(图 1.3.3-55)具有同上述类似的处理方式。闭合点模式偏移-A(图 1.3.3-56)封装了闭合点空间位置变化的一种模式。同时,在后续 Mesh 单元处理上,增加使用Weaverbird – Topological Mesh Editor⑤扩展工具。其中SubD部分可以细分 Mesh,通过单元面的细分程度可以柔滑 Mesh 获得有机(仿生)变化的形态。这是’Organic form’或’Biomimetic architecture’设计的一种途径,代码如图 1.3.3-57。
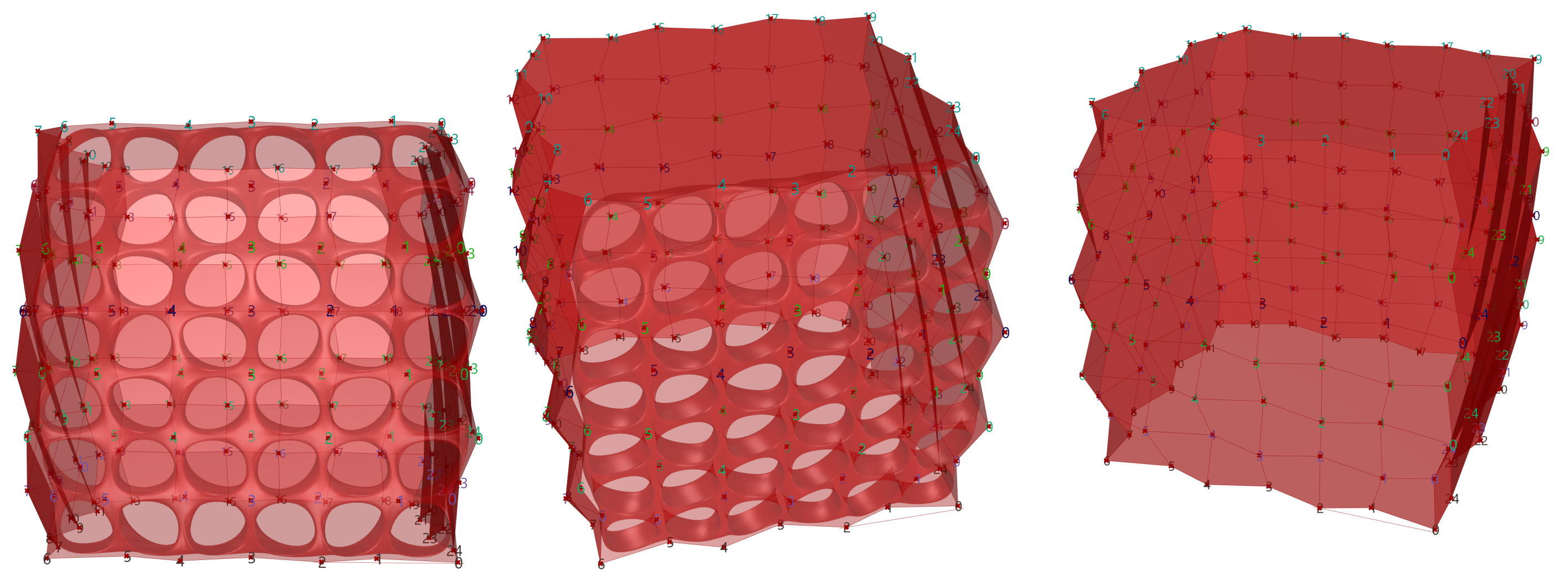
图 1.3.3-55 代码段(Mesh)-25的结果
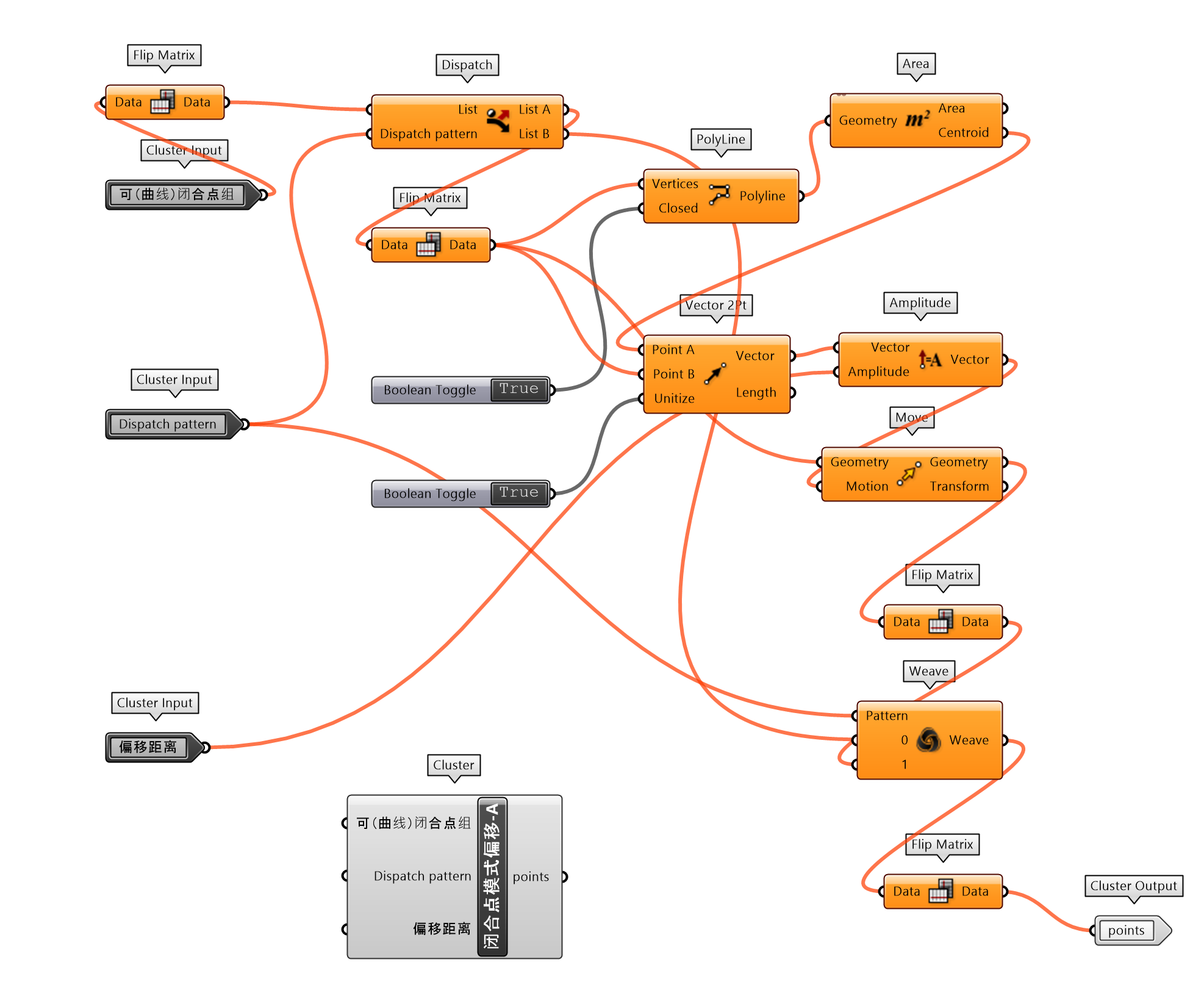
图 1.3.3-56 闭合点模式偏移-A 封装组件
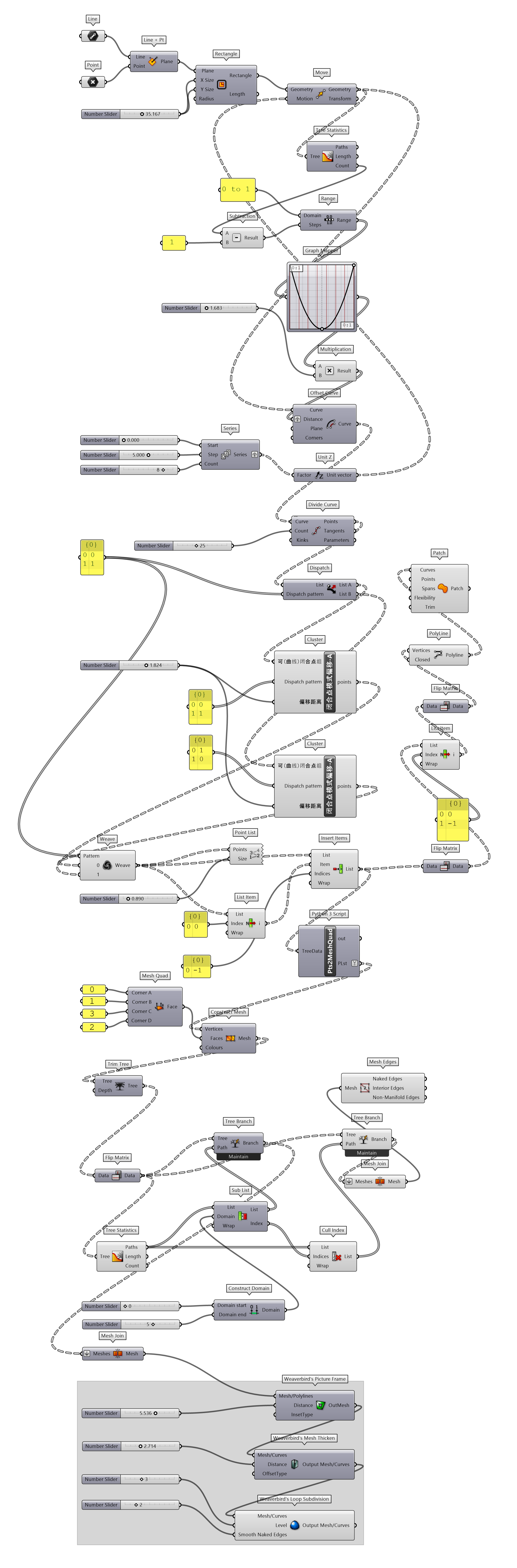
图 1.3.3-57 代码段(Mesh)-25
⇩代码下载(codeSnippet_geometry_25.gh)
🍋🟩代码段-练习-26 ( )
将可控随机间隔应用到 Mesh 的构建上如图 1.3.3-58,可以看到缩小尺度间隔时,随机尺寸单元格也并未发生重叠错乱。

图 1.3.3-58 代码段(Mesh)-26和结果:动画
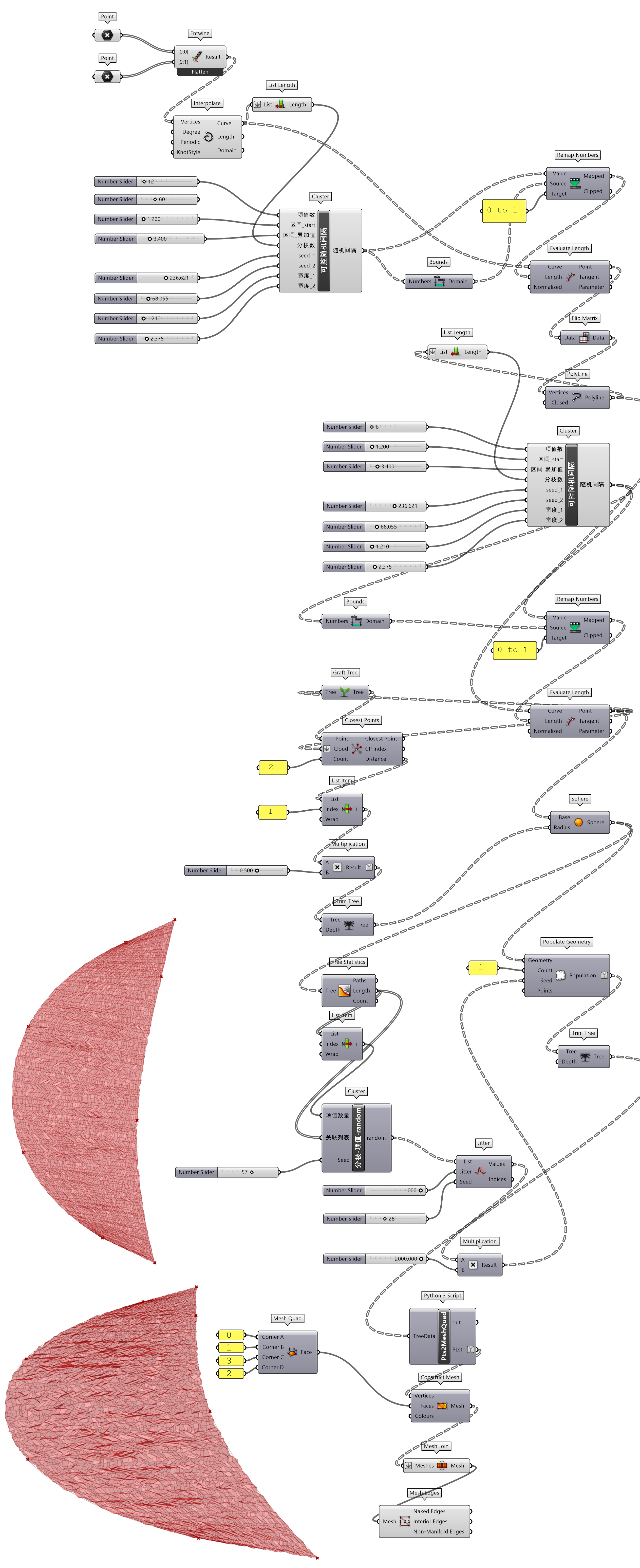
图 1.3.3-58 代码段(Mesh)-26和结果
⇩代码下载(codeSnippet_geometry_26.gh)
🍋🟩代码段-练习-27 ( )
传统置石不同于叠山,更强调石单体的形态和平面布局关系。通常要仔细推敲单个石形态,组合关系;在后续石料加工时,要根据设计的石头形式进行切割(不是寻找,也很难找到)。日本在置石艺术上很好继承了唐代的手法,并发展出自己的一套置石规则,可以查阅《作庭记》。同时,当代日本枯山水设计师枡野俊明(日本禅僧大师和日本古刹建功寺第18代主持)为当今置石艺术发展的重要人物,可以查阅《日本景观设计师枡野俊明》,从中可以获取设计及置石加工建造的方式。
参数化自动生成置石置石-A(图 1.3.3-59)和地形变化辅助地形设计-磁场工具结合进行设计的图 1.3.3-60 方案可以作为设计的一种参考,尤其在营造自然山水园时,不同的布局形式可以触发设计师的灵感。但是如果要精细推敲每一块置石形态和空间组合时,则需要使用 ‘SubD’ 等工具手工处理,或者半参数化的方式处理。
张十庆著.《作庭记-译注与研究》.天津:天津大学出版社,2004.5
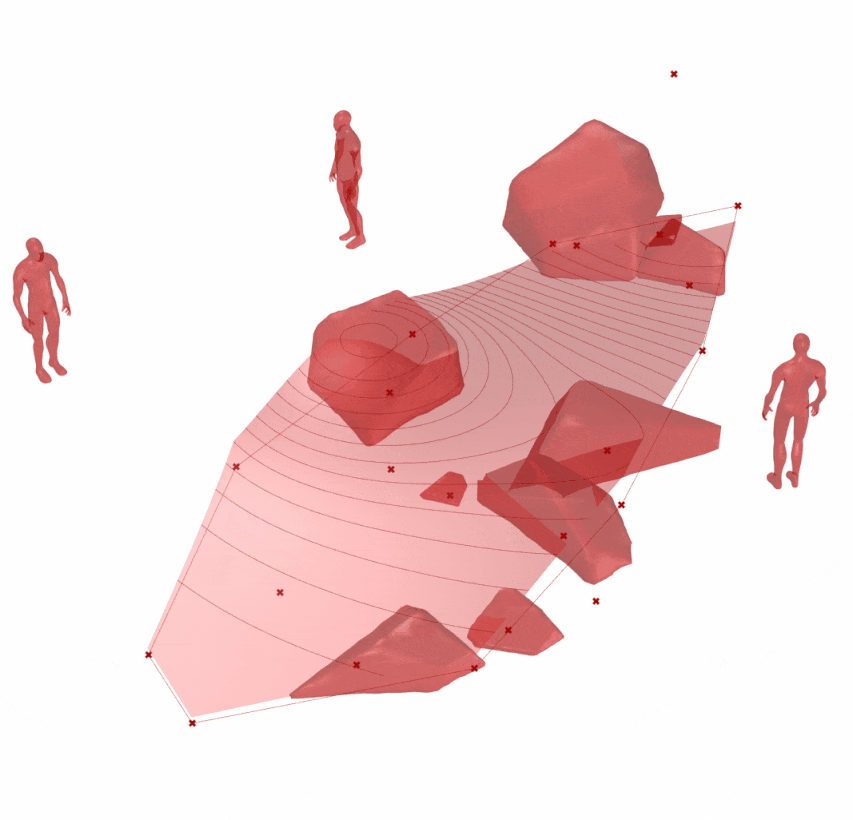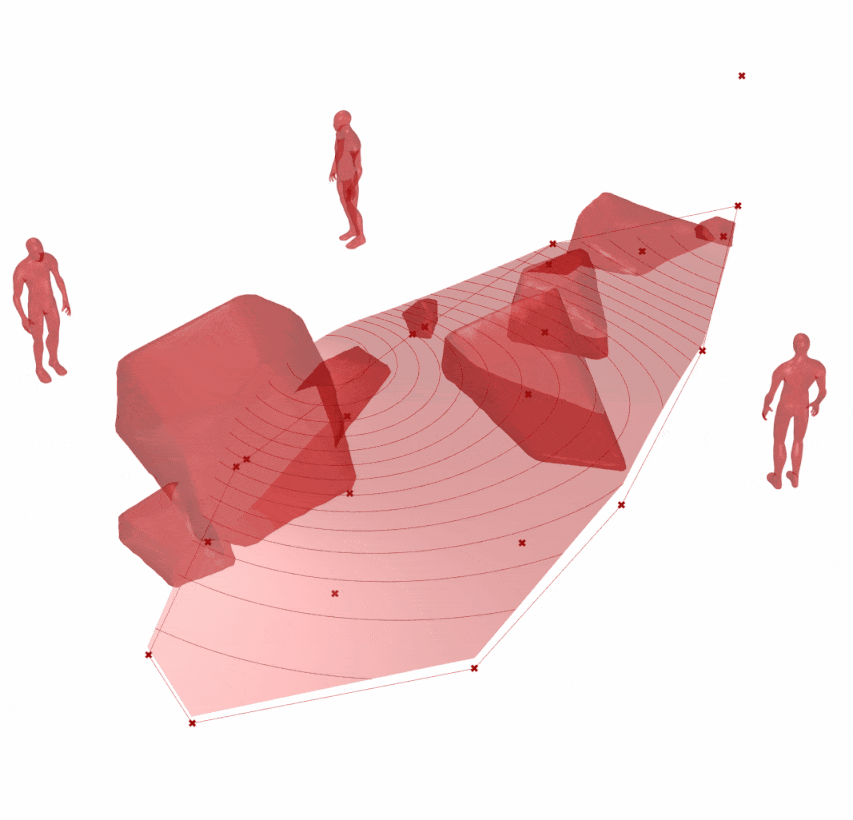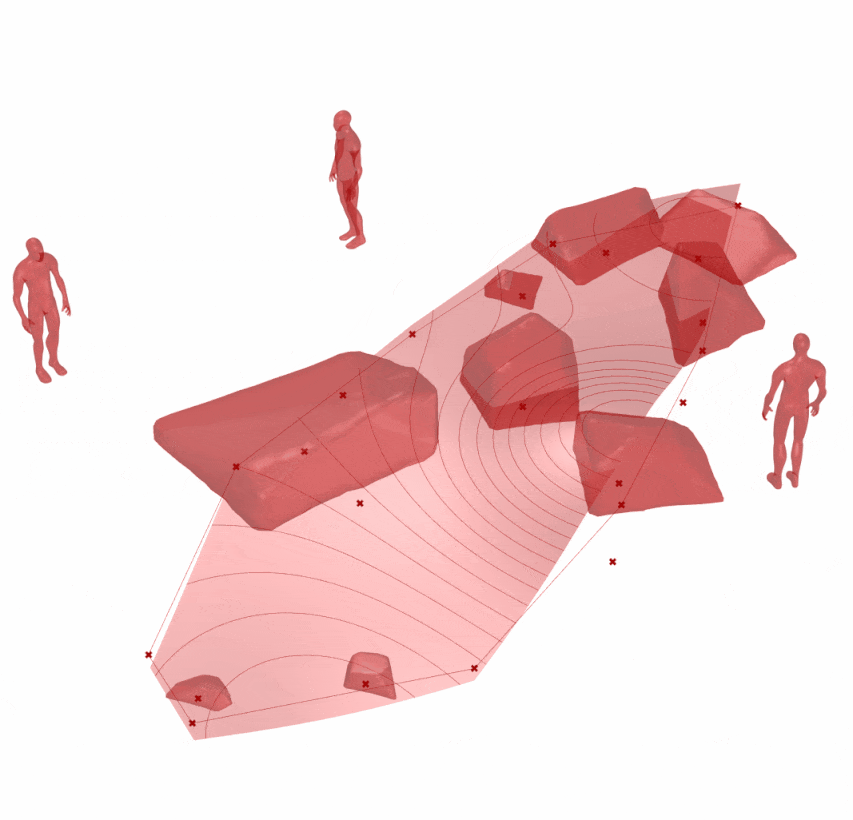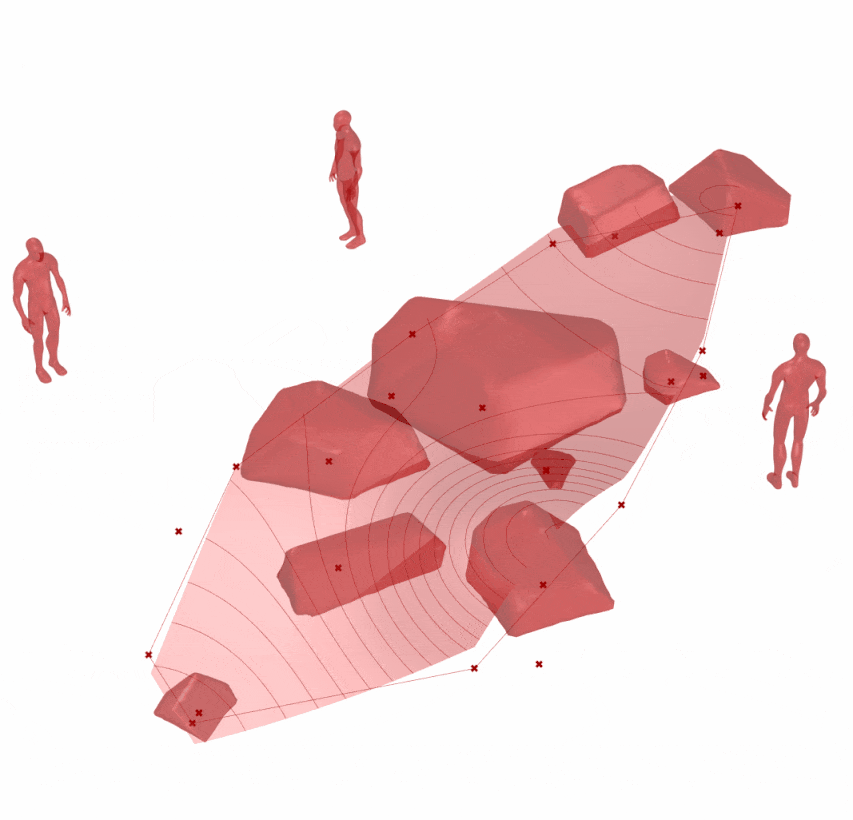
图 1.3.3-60 代码段(Mesh)-27和结果:动画
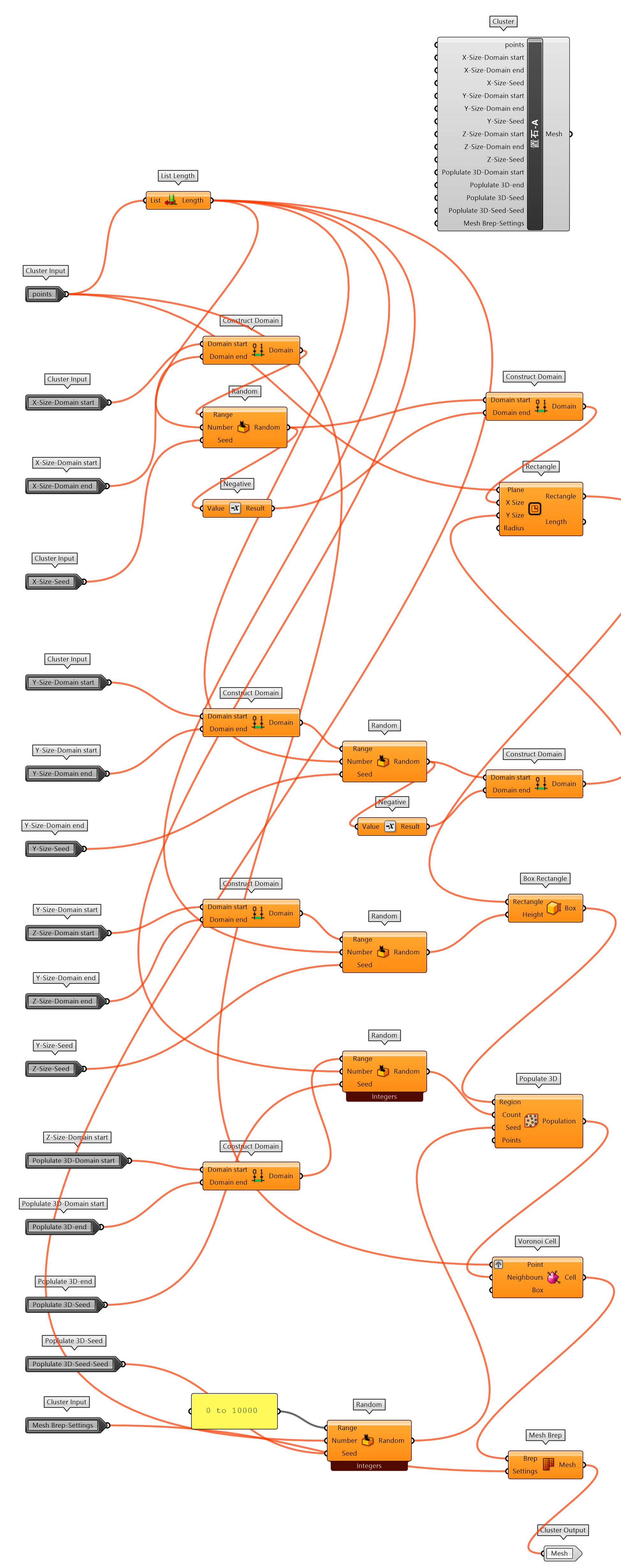
图 1.3.3-59 置石-A 封装组件
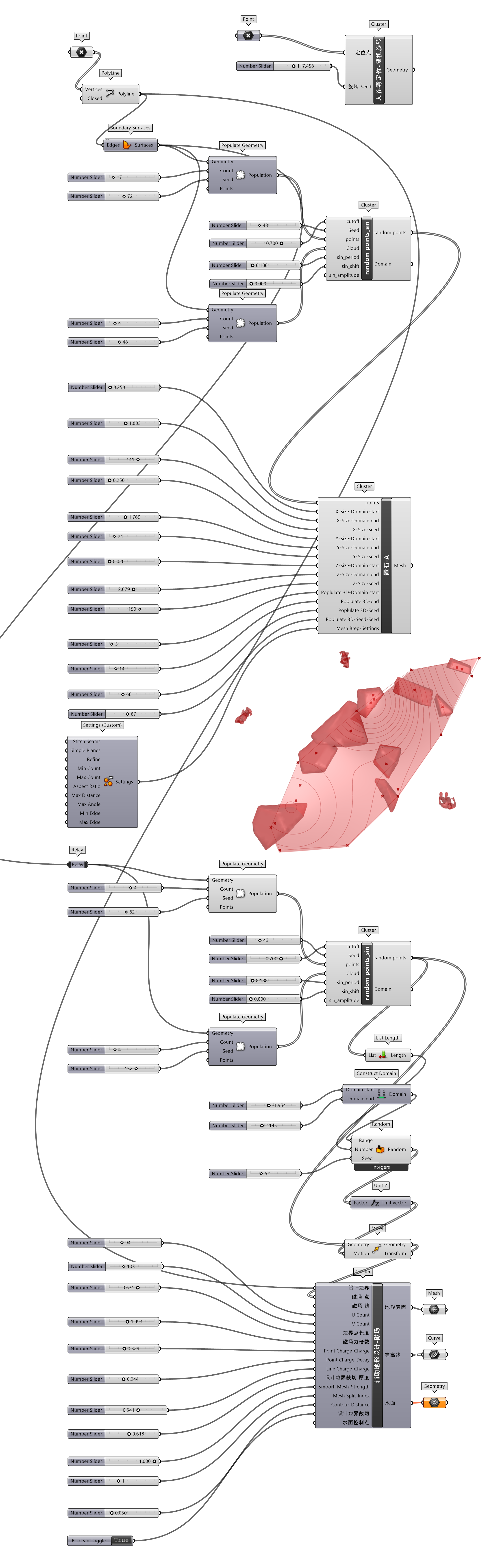
图 1.3.3-60 代码段(Mesh)-27和结果
⇩代码下载(codeSnippet_geometry_27.gh)
1.3.3.4 SubD()
SubD⑥工具也增加于 GH 中,只是 GH 版本提供的功能有限,这与 SubD 更适用于手工表面雕刻的特性有关。对于 GH 版本的 SubD 实际上更多与 Mesh 结合使用来创作出各类形态。因为 SubD 的手工雕刻特性,这里仅示范性的给出两个代码段练习。
🍋🟩代码段-练习-28 ( )
图 1.3.3-61代码段尝试将两组 Mesh 对象合并Mesh Join后,通过SubD from Mesh转换为 SubD 对象,观察结合处的变化。
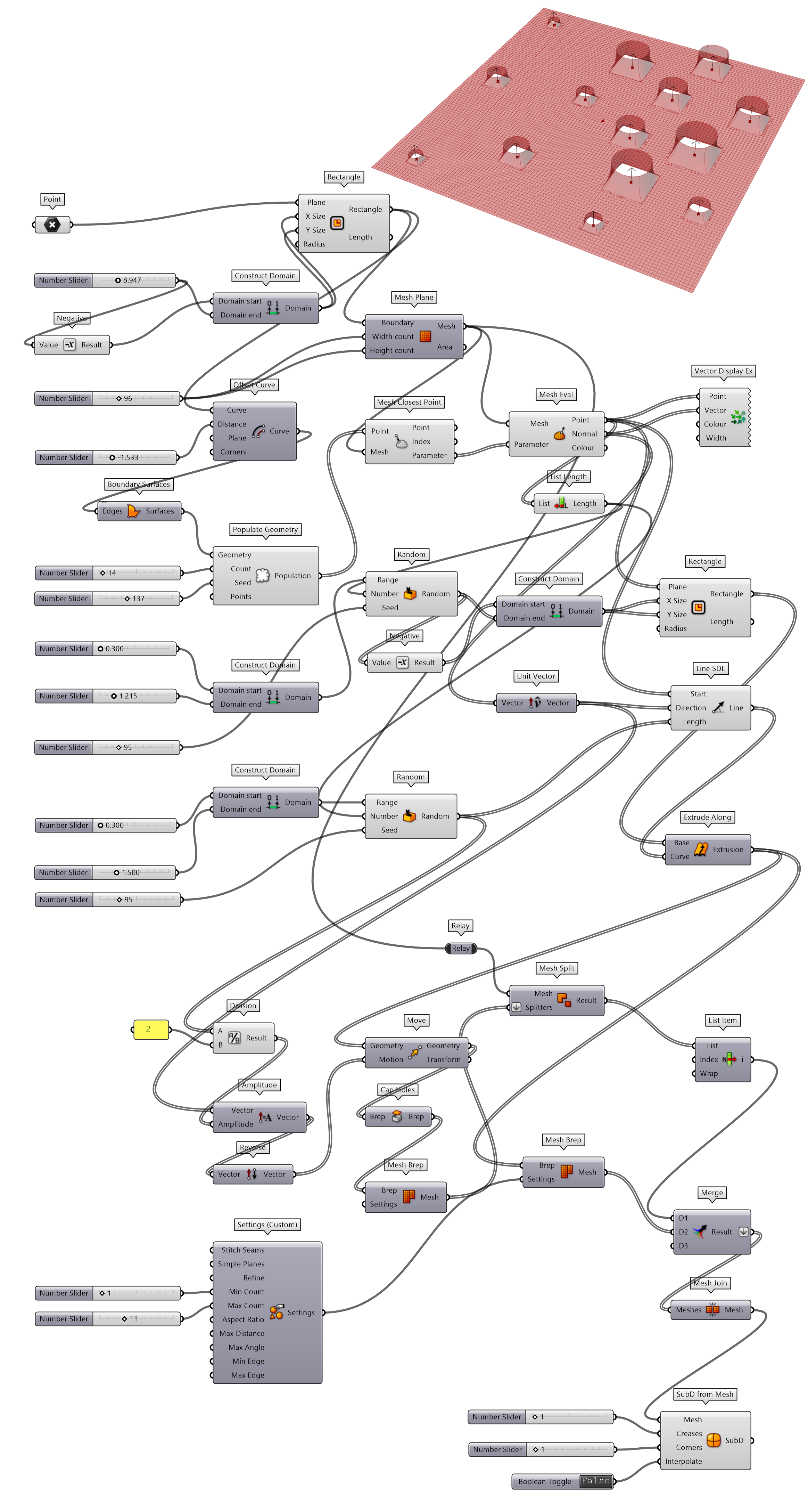
图 1.3.3-61 代码段(Mesh)-28和结果
⇩代码下载(codeSnippet_geometry_28.gh)
🍋🟩代码段-练习-29 ( )
SubD from Mesh和SubD Fuse配合,逐一融合不同的SubD对象。只是SubD Fuse输入项给出的是SubD A和SubD B,每次只能融合两个SubD对象,这使得代码编写变得繁复。其实对于类似的仿生形态处理,更多的是使用Mesh,及对Mesh进行’SubD’细分处理,例如代码段25,使用Weaverbird的SubD工具。
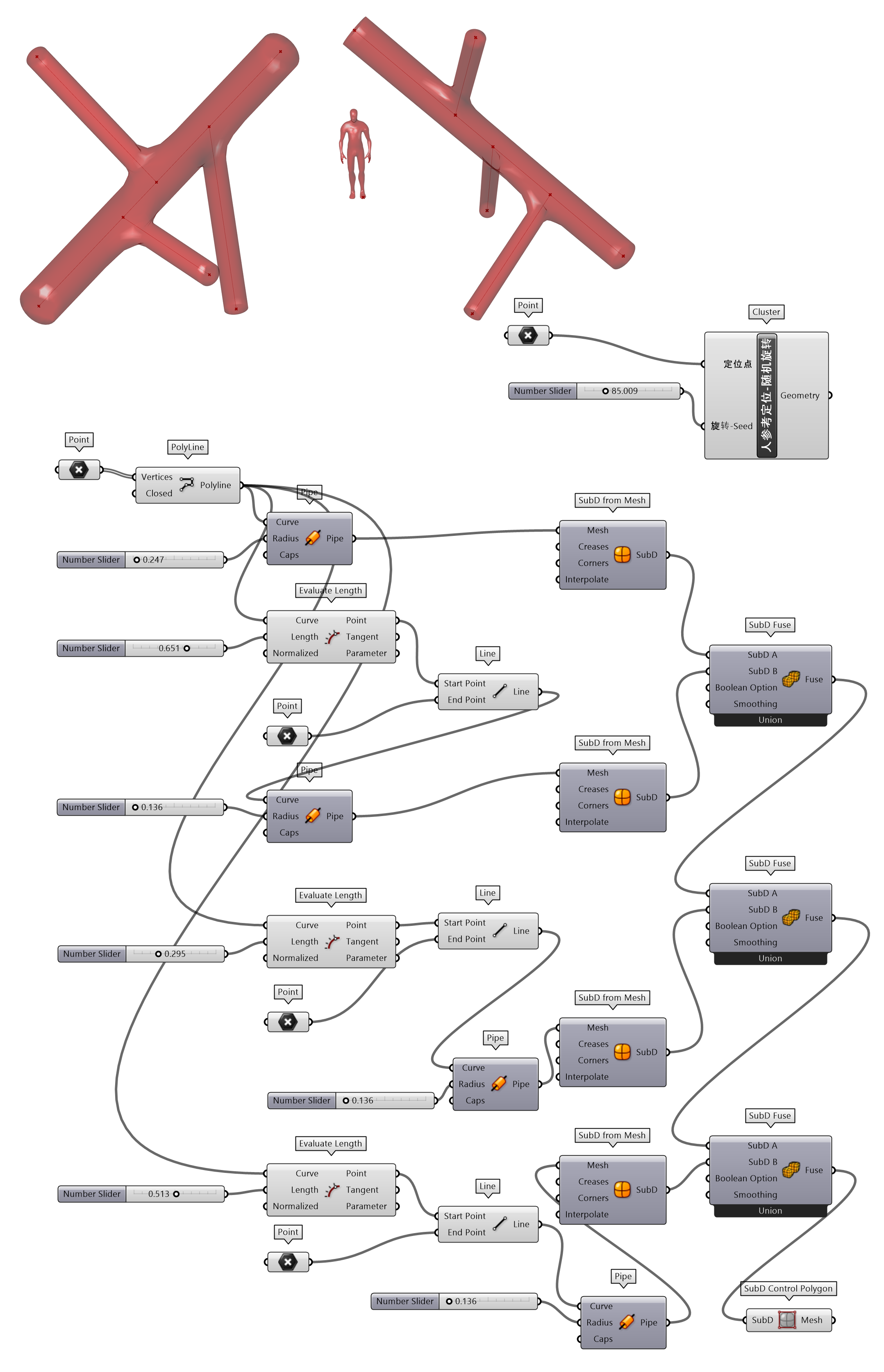
图 1.3.3-62 代码段(Mesh)-29和结果
⇩代码下载(codeSnippet_geometry_29.gh)
练习题
选择使用辅助地形设计-磁场、地形生成-磁场、磁场影响自由变换曲面、盒体随机点磁场、曲面点线控制变换、曲面点线控制变换-力大小、置石-A及本章中任何构建的工具,自行给定设计边界,自由设计。
-
必须包含
人参考定位-随机旋转,以确定设计尺度的正确性; -
磁场影响自由变换曲面、盒体随机点磁场、曲面点线控制变换、曲面点线控制变换-力大小中至少包含使用一项工具。
注释(Notes):
① Giuliano Mauri, Giuliano Mauri 是一位在世界各地工作的艺术家(https://www.giulianomauri.com/test/)。
② Procedural vegetation for BIM,分形树:指一种具有自相似性质的树状结构,其分支重复出现并且越来越细致(https://github.com/PavloMenshykh/Procedural-vegetation/blob/master/fractal_tree_source.py)。
③ LUNCHBOX,是 Grasshopper 的扩展插件,用于探索数学形状(mathematical shapes)、面板(panelling)、结构(structure)和数据管理(data management)。LunchBox 还包括一组机器学习组件,含回归、聚类和分类算法。(https://www.food4rhino.com/en/app/lunchbox)。
④ Lunchbox Grasshopper - Space Truss,Rhino Grasshopper YouTube 频道(https://www.youtube.com/watch?v=MgEpyiUO-T0&list=RDCMUCjLDKM9EzNdASaNdjBhTqug&start_radio=1&t=647s)。
⑤ Weaverbird – Topological Mesh Editor,为 Grasshopper 的扩展插件,是一个拓扑建模器(topological modeler),含有许多已知算法的细分和变化操作符,可供设计人员使用(https://www.giuliopiacentino.com/weaverbird/)。
⑥ SubD,对于需要快速探索有机形状的设计师来说,SubD 是一种新的几何类型,可以创建可编辑,高度精确的形状。与其他几何类型不同,SubD 结合了自由形式的精度,并允许同时快速编辑。(https://www.rhino3d.com/features/subd/)。